Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Enochs, Edgar
Oyonarte, Luis
and
Torrecillas, Blas
2004.
Flat Covers and Flat Representations of Quivers.
Communications in Algebra,
Vol. 32,
Issue. 4,
p.
1319.
Enochs, Edgar
and
Estrada, Sergio
2005.
Projective Representations of Quivers #.
Communications in Algebra,
Vol. 33,
Issue. 10,
p.
3467.
Estrada, Sergio
2007.
Monomial Algebras over Infinite Quivers. Applications toN-Complexes of Modules.
Communications in Algebra,
Vol. 35,
Issue. 10,
p.
3214.
Park, Sangwon
Enochs, Edgar E.
and
Kim, Hae-Sik
2009.
Injective Covers and Envelopes of Representations of Linear Quivers.
Communications in Algebra,
Vol. 37,
Issue. 2,
p.
515.
Asadollahi, J.
Eshraghi, H.
Hafezi, R.
and
Salarian, Sh.
2011.
On the homotopy categories of projective and injective representations of quivers.
Journal of Algebra,
Vol. 346,
Issue. 1,
p.
101.
Han, Juncheol
and
Park, Sangwon
2012.
PROJECTIVE REPRESENTATIONS OF A QUIVER WITH THREE VERTICES AND TWO EDGES AS R[x]-MODULES.
Korean Journal of Mathematics,
Vol. 20,
Issue. 3,
p.
343.
Rump, Wolfgang
2013.
Injective tree representations.
Journal of Pure and Applied Algebra,
Vol. 217,
Issue. 1,
p.
132.
Zhu, Haiyan
2016.
Constructing cotorsion pairs over generalized path algebras.
Frontiers of Mathematics in China,
Vol. 11,
Issue. 4,
p.
1079.
Bahiraei, P.
Hafezi, R.
and
Nematbakhsh, A.
2016.
Homotopy category of N -complexes of projective modules.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 6,
p.
2414.
Asadollahi, Javad
Hafezi, Rasool
and
Vahed, Razieh
2016.
On the Recollements of Functor Categories.
Applied Categorical Structures,
Vol. 24,
Issue. 4,
p.
331.
Eshraghi, Hossein
2017.
Representation dimension of generalized path algebras of cyclic quivers.
Communications in Algebra,
Vol. 45,
Issue. 6,
p.
2296.
Asadollahi, J.
Hafezi, R.
and
Keshavarz, M. H.
2017.
Minimal injective resolutions and Auslander-Gorenstein property for path algebras.
Communications in Algebra,
Vol. 45,
Issue. 6,
p.
2557.
Asadollahi, J.
Hafezi, R.
and
Keshavarz, M. H.
2018.
Injective representations of bound quiver algebras.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 01,
p.
1850001.
Bahlekeh, Abdolnaser
Fallah, Ali Mahin
and
Salarian, Shokrollah
2019.
Specifying the Auslander transpose in submodule category and its applications.
Kyoto Journal of Mathematics,
Vol. 59,
Issue. 1,
Holm, Henrik
and
Jørgensen, Peter
2019.
Cotorsion pairs in categories of quiver representations.
Kyoto Journal of Mathematics,
Vol. 59,
Issue. 3,
Odabaşı, Sinem
2019.
Completeness of the induced cotorsion pairs in categories of quiver representations.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 10,
p.
4536.
Estrada, Sergio
Pérez, Marco A.
and
Zhu, Haiyan
2020.
Balanced pairs, cotorsion triplets and quiver representations.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 1,
p.
67.
Vahed, Razieh
2020.
On the existence of recollements of functor categories.
Communications in Algebra,
Vol. 48,
Issue. 7,
p.
3133.
Bahiraei, Payam
2021.
Model Structures on the Category of Complexes of Quiver Representations.
Bulletin of the Iranian Mathematical Society,
Vol. 47,
Issue. S1,
p.
103.
Ju, Tengxia
and
Luo, Xiu-Hua
2021.
Strongly Gorenstein-projective Quiver
Representations.
Taiwanese Journal of Mathematics,
Vol. 25,
Issue. 3,
 $R$-modules and the injective indecomposable
$R$-modules and the injective indecomposable
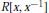 $R[\text{x},\,{{\text{x}}^{-1}}]$ -modules.
$R[\text{x},\,{{\text{x}}^{-1}}]$ -modules.

