Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:13:51.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy Decompositions Involving the Loops of Coassociative 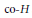$co-H$ Spaces

Published online by Cambridge University Press:  20 November 2018

Stephen D. Theriault
Stephen D. Theriault*
Affiliation:
University of Virginia, Charlottesville, Virginia, 22904, U.S.A., e-mail: [email protected]
*
Current address: University of Aberdeen Aberdeen, AB24 3UE, United Kingdom, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

James gave an integral homotopy decomposition of 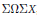$\sum \Omega \sum X$, Hilton-Milnor one for 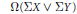$\Omega (\sum X\,\vee \,\sum Y)$, and Cohen-Wu gave 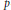$p$-local decompositions of 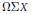$\Omega \sum X$ if 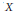$X$ is a suspension. All are natural. Using idempotents and telescopes we show that the James and Hilton-Milnor decompositions have analogues when the suspensions are replaced by coassociative 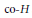$\text{co-}H$ spaces, and the Cohen-Wu decomposition has an analogue when the (double) suspension is replaced by a coassociative, cocommutative 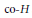$\text{co-}H$ space.

Keywords

55P3555P45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 181 - 203
Copyright
Copyright © Canadian Mathematical Society 2003

References

[B1] Berstein, I., A note on spaces with nonassociative comultiplication. Proc. Cambridge Philos. Soc. 60 (1964), 353–354.Google Scholar
[B2] Berstein, I., On cogroups in the category of graded algebras. Trans. Amer.Math. Soc. 115 (1965), 257–269.Google Scholar
[BH] Berstein, I. and Harper, J. R., Cogroups which are not suspensions. Algebraic Topology (Arcata 1986), 63–86, Lecture Notes in Math. 1370(1989).Google Scholar
[CT] Cohen, F. R. and Taylor, L. R., The homology of function spaces. Math. Z. 198 (1988), 299–316.Google Scholar
[CW] Cohen, F. R. and Wu, J., A remark on the homotopy groups of ∑nRp2 . The Čech Centennial, 65–81, Contemp.Math. 181(1995).Google Scholar
[Ga] Ganea, T., Cogroups and suspensions. Invent.Math. 9 (1970), 185–197.Google Scholar
[Gr1] Gray, B., EHP spectra and periodicity I: geometric constructions. Trans. Amer. Math. Soc. 340 (1993), 595–616.Google Scholar
[Gr2] Gray, B., Associativity in two-cell complexes. Geometry and Topology: Aarhus (1998), 185–196, Contemp.Math. 258(2000).Google Scholar
[J] Jacobson, N., Lie Algebras. Dover, 1962.Google Scholar
[R] Rutter, J. W., The suspension of the loops on a space with comultiplication.Math. Ann. 209 (1974), 69–82.Google Scholar
[T] Theriault, S. D., A reconstruction of Anick's fibration. Submitted.Google Scholar