Article contents
Homological Aspects of Semigroup Gradings on Rings and Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
This article studies algebras  $R$ over a simple artinian ring
$R$ over a simple artinian ring 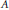 $A$, presented by a quiver and relations and graded by a semigroup
$A$, presented by a quiver and relations and graded by a semigroup  $\Sigma $. Suitable semigroups often arise from a presentation of
$\Sigma $. Suitable semigroups often arise from a presentation of  $R$. Throughout, the algebras need not be finite dimensional. The graded
$R$. Throughout, the algebras need not be finite dimensional. The graded
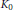 ${{K}_{0}}$, along with the
${{K}_{0}}$, along with the  $\Sigma $-graded Cartan endomorphisms and Cartan matrices, is examined. It is used to study homological properties.
$\Sigma $-graded Cartan endomorphisms and Cartan matrices, is examined. It is used to study homological properties.
A test is found for finiteness of the global dimension of a monomial algebra in terms of the invertibility of the Hilbert  $\Sigma $-series in the associated path incidence ring.
$\Sigma $-series in the associated path incidence ring.
The rationality of the  $\Sigma $-Euler characteristic, the Hilbert
$\Sigma $-Euler characteristic, the Hilbert  $\Sigma $-series and the Poincaré-Betti
$\Sigma $-series and the Poincaré-Betti  $\Sigma $-series is studied when
$\Sigma $-series is studied when  $\Sigma $ is torsion-free commutative and
$\Sigma $ is torsion-free commutative and 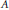 $A$ is a division ring. These results are then applied to the classical series. Finally, we find new finite dimensional algebras for which the strong no loops conjecture holds.
$A$ is a division ring. These results are then applied to the classical series. Finally, we find new finite dimensional algebras for which the strong no loops conjecture holds.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
- 3
- Cited by


