Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-02T23:01:57.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic Mappings of the Hyperbolic Space into the Complex Euclidean Space and the Bloch Theorem

Published online by Cambridge University Press:  20 November 2018

Kyong T. Hahn
Kyong T. Hahn*
Affiliation:
The Pennsylvania State University, University Park, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is to study various properties of holomorphic mappings defined on the unit ball B in the complex euclidean space Cn with ranges in the space Cm. Furnishing B with the standard invariant Kähler metric and Cm with the ordinary euclidean metric, we define, for each holomorphic mapping f : B → Cm, a pair of non-negative continuous functions qf and Qf on B ; see § 2 for the definition.

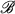Let (Ω), Ω > 0, be the family of holomorphic mappings f : B → Cn such that Qf(z) ≦ Ω for all z ∈ B. 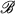(Ω) contains the family 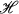(M) of bounded holomorphic mappings as a proper subfamily for a suitable M > 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 2 , 01 April 1975 , pp. 446 - 458
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Anderson, J. M., Clunie, J., and Ch. Pommerenke, On Block functions and normal functions, J. Reine Angew Math. 270 (1974), 12–37.Google Scholar
2. Barth, T. J., Taut and tight complex manifolds, Proc. Amer. Math. Soc. 24 (1970), 429–431.Google Scholar
3. Hahn, K. T., The non-euclidean Pythagorean theorem with respect to the Bergman metric, Duke Math. J. 33 (1966), 523–534.Google Scholar
4. Hahn, K. T., Higher dimensional generalization of the Bloch constant and their lower bounds, Trans. Amer. Math. Soc. 179 (1973), 263–274.Google Scholar
5. Hahn, K. T., Quantitative Bloch's theorem for certain classes of holomorphic mappings of the ball into Pn(C) (to appear).Google Scholar
6. Kobayashi, S. and Nomizu, K., Foundations of differential geometry, Vol. 2 (Interscience, New York, 1969).Google Scholar
7. Kobayashi, S., Hyperbolic manifolds and holomorphic mappings (Marcel Dekker, New York, 1970).Google Scholar
8. Landau, E., Ûber die Blochsche Konstante und zwei verwandte Weltkonstanten, Math. Z. 30 (1920), 608–634.Google Scholar
9. Lehto, O. and Virtanen, K. J., Boundary behaviour and normal metvmorphic functions, Acta Math. 97 (1957), 47–65.Google Scholar
10. L∞k, K. H., Schwarz lemma and analytic invariants, Sci. Sinica 7 (1958), 453–504.Google Scholar
11. Seidel, W. and Walsh, J. L., On the derivative of functions analytic in the unit circle and their radii of univalence and of p-valence, Trans. Amer. Math. Soc. 52 (1942), 129–216.Google Scholar
12. Veech, W. A., A second course in complex analysis (Benjamin, New York, 1967).Google Scholar
13. Wu, H., Normal families of holomorphic mappings, Acta Math. 119 (1967), 193–233.Google Scholar