Article contents
Holomorphic Functions with Positive Real Part
Published online by Cambridge University Press: 20 November 2018
Extract
The main purpose of this note is to prove a special case of the following conjecture.
Conjecture. If F is holomorphic on the unit ball Bn in Cn and has positive real part, then F is in Hp(Bn) for 0 < p < ½(n + 1).
Here Hp(Bn) (0 < p < ∞) denote the usual Hardy spaces of holomorphic functions on Bn. See below for definitions. We remark that the conjecture is known for 0 < p < 1 and that some evidence for it already exists in the literature; for example [1, Theorems 3.11 and 3.15] where it is shown that a particular extreme element of the convex cone of functions
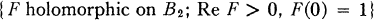
is in Hp(B2) for 0 < p < 3/2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
- 1
- Cited by


