Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T06:30:12.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Order Tangents to Analytic Varieties along Curves

Published online by Cambridge University Press:  20 November 2018

Rüdiger W. Braun ,
Reinhold Meise  and
B. A. Taylor
Rüdiger W. Braun
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität Universitätsstraße 1, 40225 Düsseldorf, Germany, email: [email protected]
Reinhold Meise
Affiliation:
Mathematisches Institut Heinrich-Heine-Universität Universitätsstraße 1 40225 Düsseldorf Germany, email: [email protected]
B. A. Taylor
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 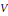$V$ be an analytic variety in some open set in 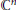${{\mathbb{C}}^{n}}$ which contains the origin and which is purely 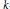$k$-dimensional. For a curve $\gamma $ in 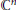${{\mathbb{C}}^{n}}$, defined by a convergent Puiseux series and satisfying 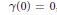$\gamma (0)\,=\,0$, and 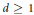$d\,\ge \,1$, define 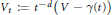${{V}_{t}}\,:=\,{{t}^{-d}}\,\left( V\,-\,\gamma \left( t \right) \right)$. Then the currents defined by 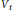${{V}_{t}}$ converge to a limit current 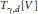${{T}_{\gamma ,d}}\left[ V \right]$ as $t$ tends to zero. 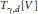${{T}_{\gamma ,d}}\left[ V \right]$ is either zero or its support is an algebraic variety of pure dimension 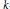$k$ in 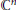${{\mathbb{C}}^{n}}$. Properties of such limit currents and examples are presented. These results will be applied in a forthcoming paper to derive necessary conditions for varieties satisfying the local Phragmén-Lindelöf condition that was used by Hörmander to characterize the constant coefficient partial differential operators which act surjectively on the space of all real analytic functions on 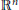${{\mathbb{R}}^{n}}$.

Keywords

32C25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 64 - 90
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bishop, E., Condition for the analyticity of certain sets. Michigan Math J. 11 (1964), 289–304.Google Scholar
[2] Braun, R. W., Hörmander's Phragmén-Lindelöf principle and irreducible singularities of codimension 1. Boll. Un. Mat. Ital. A (7) 6 (1992), 339–348.Google Scholar
[3] Braun, R. W., Meise, R. and Taylor, B.A., Algebraic varieties on which the classical Phragmén-Lindelöf estimates hold for plurisubharmonic functions. Math. Z. 232 (1999), 103–135.Google Scholar
[4] Braun, R. W., Meise, R. and Taylor, B. A., Characterization of the homogeneous polynomials P for which (p + Q)(D) admits a continuous linear right inverse for all lower order perturbations Q. Pacific J. Math. 192 (2000), 201–218.Google Scholar
[5] Braun, R. W., Meise, R. and Taylor, B. A., The geometry of analytic varieties satisfying the local Phragmén-Lindelöf condition and a geometric characterization of partial differential operators that are surjective on A(R4). Preprint.Google Scholar
[6] Chirka, E. M., Complex Analytic Sets. Kluwer, Dordrecht, 1989 (translated from the Russian).Google Scholar
[7] Hörmander, L., On the existence of real analytic solutions of partial differential equations with constant coefficients. Invent.Math. 21 (1973), 151–183.Google Scholar
[8] Meise, R., Taylor, B. A. and Vogt, D., Extremal plurisubharmonic functions of linear growth on algebraic varieties. Math. Z. 219 (1995), 515–537.Google Scholar
[9] Meise, R., Taylor, B. A. and Vogt, D., Phragmén-Lindelöf principles on algebraic varieties. J. Amer.Math. Soc. 11 (1998), 1–39.Google Scholar
[10] Stoll, W., The growth of the area of a transcendental analytic set. Math. Ann. 156 (1964), 47–78, 144–170.Google Scholar
[11] Whitney, H., Complex analytic varieties. Addison-Wesley, Reading, Mass., 1972.Google Scholar