Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T08:03:23.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Connectedness Properties of Support Points and Functionals of Convex Sets

Published online by Cambridge University Press:  20 November 2018

Carlo Alberto De Bernardi
Carlo Alberto De Bernardi*
Affiliation:
Dipartimento di Matematica, Università degli Studi di Milano, Via C. Saldini 50, 20133 Milano, Italy, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the set of all support points of a nonempty closed convex bounded set 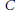$C$ in a real infinite-dimensional Banach space 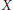$X$ is 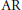$\text{AR}$(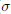$\sigma $-compact) and contractible. Under suitable conditions, similar results are proved also for the set of all support functionals of 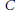$C$ and for the domain, the graph, and the range of the subdifferential map of a proper convex lower semicontinuous function on 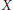$X$.

Keywords

46A5546B9952A07convex setsupport pointsupport functionalabsolute retractLeray-Schauder continuation principle
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 6 , 01 December 2013 , pp. 1236 - 1254
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bessaga, C. and Pelczyński, A., Selected topics in infinite-dimensional topology. Monografie Matematyczne, 58, PWN—Polish Scientific Publishers,Warsaw, 1975.Google Scholar
[2] Bishop, E. and Phelps, R. R., The support functionals of a convex set. Proc. Sympos. Pure Math., 7, American Mathematical Society, Providence, RI, 1963, pp. 27–35.Google Scholar
[3] Corson, H. and Klee, V, Topological classification of convex sets. Proc. Sympos. Pure Math., 7, American Mathematical Society, Providence, RI, 1963, pp. 37–51.Google Scholar
[4] De Bernardi, C. and Veselý, L., On support points and support functionals of convex sets. Israel J. Math. 171(2009), 15–27. http://dx.doi.org/10.1007/s11856-009-0037-6 Google Scholar
[5] Dugundji, J., An extension of Tietze's theorem. Pacific J. Math. 1(1951), 353–367.Google Scholar
[6] Dugundji, J., Topology. Allyn and Bacon, Inc., Boston, Mass. 1966.Google Scholar
[7] Engelking, R., General topology. Second ed., Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[8] Fabian, M., Habala, P., Hájek, P., Montesinos, V., and Zizler, V., Banach space theory. The basis for linear and nonlinear analysis. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer, New York, 2011.Google Scholar
[9] Granas, A. and Dugundji, J., Fixed point theory. Springer Monographs in Mathematics, Springer-Verlag, New York, 2003.Google Scholar
[10] Luna, G., Connectedness properties of support points of convex sets. Rocky Mountain J. Math. 16(1986), no. 1, 147–151. http://dx.doi.org/10.1216/RMJ-1986-16-1-147 Google Scholar
[11] Luna, G., Local connectedness of support points. Rocky Mountain J. Math. 18(1988), no. 1, 179–184. http://dx.doi.org/10.1216/RMJ-1988-18-1-179 Google Scholar
[12] Michael, E., Continuous selections. I. Ann. of Math. (2) 63(1956), 361–382. http://dx.doi.org/10.2307/1969615 Google Scholar
[13] Phelps, R. R., Some topological properties of support points of convex sets. Proceedings of the International Symposium on Partial Differential Equations and the Geometry of Normed Linear Spaces (Jerusalem, 1972). Israel J. Math. 13(1972), 327–336. http://dx.doi.org/10.1007/BF02762808 Google Scholar
[14] Phelps, R. R., Convex functions, monotone operators and differentiability. Second ed., Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1993.Google Scholar
[15] Veselá, L., A parametric smooth variational principle and support properties of convex sets and functions. J. Math. Anal. Appl. 350(2009), 550–561. http://dx.doi.org/10.1016/j.jmaa.2008.03.005 Google Scholar