Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-08T19:27:27.331Z Has data issue: false hasContentIssue false
  • English
  • Français

The Heat Equation on the Spaces of Positive Definite Matrices

Published online by Cambridge University Press:  20 November 2018

P. Sawyer
P. Sawyer*
Affiliation:
Department of Mathematics University of Ottawa Ottawa, Ontario K1N6N5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main topic of this paper is the study of the fundamental solution of the heat equation for the symmetric spaces of positive definite matrices, Pos(n,R).

Our first step is to develop a “False Abel Inverse Transform” which transforms functions of compact support on an euclidean space into integrable functions on the symmetric space. The transform is shown to satisfy the relation 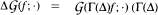is the usual Laplacian with a constant drift).

Using this transform, we find explicit formulas for the heat kernel in the cases n = 2 and n = 3. These formulas allow us to give the asymptotic development for the heat kernel as t tends to infinity. Finally, we give an upper and lower bound of the same type for the heat kernel.

Keywords

58G30(53C35,58G11)
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 3 , 01 June 1992 , pp. 624 - 651
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Anker, Jean-Philippe, La forme exacte de l'estimation fondamentale de Harish-Chandra, Acad C.R. Sci. Paris Sér. I Math. 305 (1987), 371–374.Google Scholar
2. Anker, Jean-Philippe, Le noyau de la chaleur sur les espaces symétriques U(p, q)/ U(p) x U(q), Lecture Notes in Math. 1359, Springer Verlag, New-York, 1988.60–82.Google Scholar
3. Chayet, Maurice, Some general estimates for the heat kernel on symmetric spaces and related problems of integral geometry, Thesis, McGill University, (1990).Google Scholar
4. Davies, E.B., Heat kernels and spectral theory, Cambridge Univ. Press, (1989).Google Scholar
5. Gelfand, M. and Naimark, M.A., Unitàre Darstellung der klassichen Gruppen, Akademie-Verlag, Berlin, 1957.Google Scholar
6. Gangolli, R., Asymptotic behaviour of spectra of compact quotients of certain symmetric spaces, Acta Math. 121 (1968), 151–192.Google Scholar
7. Helgason, Sigurdur, Differential Geometry, Lie Groups and Symmetric spaces, Academic Press, New York, 1978.Google Scholar
8. Helgason, Sigurdur, Group and Geometric Analysis, Academic Press, New York, 1984.Google Scholar
9. Herz, Carl S., Les espaces symétriques pour piétons, Publications mathématiques d'Orsay, Séminaire d'analyse harmonique, 1978–1979.Google Scholar
10. Carl S.|Herz, I.,The Poisson kernel for sl(3, R), Lecture Notes in Math. 1096, Springer Verlag, New-York, 1984. 333–346.Google Scholar
11. Koornwinder, T.H., Jacobi transformations and analysis on noncompactsemisimple Lie groups. In: Special functions: group theoretical aspects and applications, Askey, R.A. & al. (eds), Reidel, (1984).Google Scholar
12. Lohoué, Noël and Rychener, Thomas, Die Resolvente von A auf symmetrischen Raumen vom nichtkompakten Typ, Comment. Math. Helv. 57 (1982), 445–46.Google Scholar
13. Bhanu, T.S. Murti, Plancherel's measure for the factor space SL(n;R)/ SO(n;R), Soviet Math. Dokl. 1 (1960), 860–862.Google Scholar
14. Sawyer, Patrice, The Heat Equation on the Symmetric Space associated with SL{n, R), Thesis, McGill University, (1989).Google Scholar