Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T09:51:18.427Z Has data issue: false hasContentIssue false
  • English
  • Français

The H and K Family of Mock Theta Functions

Published online by Cambridge University Press:  20 November 2018

Richard J. McIntosh
Richard J. McIntosh*
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK S4S 0A2 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

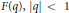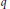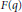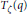In his last letter to Hardy, Ramanujan defined 17 functions $F\left( q \right),\,\left| q \right|\,<\,1$, which he called mock $\theta $-functions. He observed that as $q$ radially approaches any root of unity $\zeta $ at which $F\left( q \right)$ has an exponential singularity, there is a $\theta $-function ${{T}_{\zeta }}\left( q \right)$ with 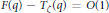$F\left( q \right)\,-\,{{T}_{\zeta }}\left( q \right)\,=\,O\left( 1 \right)$. Since then, other functions have been found that possess this property. These functions are related to a function 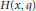$H\left( x,\,q \right)$, where $x$ is usually 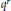${{q}^{r}}$ or 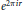${{e}^{2\pi ir}}$ for some rational number $r$. For this reason we refer to 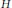$H$ as a “universal” mock $\theta $-function. Modular transformations of 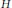$H$ give rise to the functions 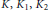$K,\,{{K}_{1}},\,{{K}_{2}}$. The functions 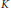$K$ and 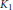${{K}_{1}}$ appear in Ramanujan's lost notebook. We prove various linear relations between these functions using Appell–Lerch sums (also called generalized Lambert series). Some relations (mock theta “conjectures”) involving mock $\theta $-functions of even order and 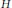$H$ are listed.

Keywords

11B6533D15mock theta functionq-seriesAppell–Lerch sumgeneralized Lambert series
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 935 - 960
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Andrews, G. E. and Berndt, B. C., Ramanujan's lost notebook. Part I. Springer, New York, 2005.Google Scholar
[2] Andrews, G. E. and Hickerson, D., Ramanujan's “lost” notebook. VII. The sixth order mock theta functions. Adv. Math. 89(1991), no. 1, 60–105. http://dx.doi.org/10.1016/0001-8708(91)90083-J Google Scholar
[3] Apostol, T. M., Modular functions and Dirichlet series in number theory. Second ed., Graduate Texts in Mathematics, Springer-Verlag, New York, 1990.Google Scholar
[4] Bringmann, K. and Ono, K., Dyson's ranks and Maass forms. Ann. of Math. 171(2010), no. 1, 419–449. http://dx.doi.org/10.4007/annals.2010.171.419 Google Scholar
[5] Bringmann, K., Ono, K., and Rhoades, R., Eulerian series as modular forms. J. Amer. Math. Soc. 21(2008), no. 4, 1085–1104. http://dx.doi.org/10.1090/S0894-0347-07-00587-5 Google Scholar
[6] Choi, Y.-S., Tenth order mock theta functions in Ramanujan's lost notebook. Invent. Math. 136(1999), no. 3, 497–569. http://dx.doi.org/10.1007/s002220050318 Google Scholar
[7] Gasper, G. and Rahman, M., Basic hypergeometric series. Encyclopedia of Mathematics and its Applications, 35, Cambridge University Press, Cambridge, 1990.Google Scholar
[8] Garvan, F. G., New combinatorial interpretations of Ramanujan's partition congruences mod 5, 7 and 11. Trans. Amer. Math. Soc. 305(1988), no. 1, 47–77.Google Scholar
[9] Göllnitz, H., Partitionen mit Differenzenbedingungen. J. Reine Angew. Math. 225(1967), 154–190. http://dx.doi.org/10.1515/crll.1967.225.154 Google Scholar
[10] Gordon, B., Some continued fractions of the Rogers-Ramanujan type. Duke Math. J. 32(1965), 741–748. http://dx.doi.org/10.1215/S0012-7094-65-03278-3 Google Scholar
[11] Gordon, B. and Mc Intosh, R. J., Some eighth order mock theta functions. J. London Math. Soc. (2) 62(2000), no. 2, 321–335. http://dx.doi.org/10.1112/S0024610700008735 Google Scholar
[12] Gordon, B. and Mc Intosh, R. J., Modular transformations of Ramanujan's fifth and seventh order mock theta functions. Ramanujan J. 7(2003), no. 1–3, 193–222. http://dx.doi.org/10.1023/A:1026299229509 Google Scholar
[13] Gordon, B. and Mc Intosh, R. J., A survey of classical mock theta functions. To appear, Developments in Mathematics, Springer 2011.Google Scholar
[14] Gordon, B. and Mc Intosh, R. J., Some identities for Appell-Lerch sums and a universal mock theta function. Ramanujan J., to appear.Google Scholar
[15] Hickerson, D., A proof of the mock theta conjectures. Invent. Math. 94(1988), no. 3, 639–660. http://dx.doi.org/10.1007/BF01394279 Google Scholar
[16] Hickerson, D., On the seventh order mock theta functions. Invent. Math. 94(1988), no. 3, 661–677. http://dx.doi.org/10.1007/BF01394280 Google Scholar
[17] Kang, S.-Y., Mock Jacobi forms in basic hypergeometric series. Compos. Math. 145(2009), no. 3, 553–565. http://dx.doi.org/10.1112/S0010437X09004060 Google Scholar
[18] Lerch, M., Poznámky k theorii funkćı elliptickych. Rozpravy České Akademie Ćısaře Františka Josefa pro vědy, slovesnost a uměńı v praze, 24(1892), 465–480.Google Scholar
[19] Lerch, M., Nová analogie řady theta a některé zvláštńı hypergeometrické řady Heineovy. Rozpravy 3(1893), 1–10.Google Scholar
[20] Mc Intosh, R. J., Second order mock theta functions. Canad. Math. Bull. 50(2007), no. 2, 284–290. http://dx.doi.org/10.4153/CMB-2007-028-9 Google Scholar
[21] Mordell, L. J., The definite integral and the analytic theory of numbers. Acta. Math. 61(1933), no. 1, 323–360. http://dx.doi.org/10.1007/BF02547795 Google Scholar
[22] Ramanujan, S., Collected papers. Cambridge University Press, 1927; reprinted Chelsea, New York, 1962.Google Scholar
[23] Ramanujan, S., The lost notebook and other unpublished papers. Springer-Verlag, Berlin; Narosa, New Delhi, 1988.Google Scholar
[24] Slater, L. J., Further identities of the Rogers-Ramanujan type. Proc. London Math. Soc. (2) 54(1952), 147–167. http://dx.doi.org/10.1112/plms/s2-54.2.147 Google Scholar
[25] Tannery, J. and Molk, J., Éléments de la théorie des fonctions elliptiques. Tomes I–IV, Gauthier-Villars, Paris, 1893–1902; reprinted, Chelsea, New York, 1972.Google Scholar
[26] Watson, G. N., The final problem: an account of the mock theta functions. In: Ramanujan: essays and surveys, Hist. Math., 22, American Mathematical Society, Providence, RI, 2001, pp. 325–347.Google Scholar
[27] Whittaker, E. T. and Watson, G. N., A course of modern analysis. 4th ed., Cambridge University Press, 1952.Google Scholar
[28] Zagier, D., Ramanujan's mock theta functions and their applications (d’après Zwegers and Bringmann-Ono). Séminaire Bourbaki, 60ème année, 2006–2007 no. 986.Google Scholar
[29] Zwegers, S. P., Mock theta functions. Ph. D. Thesis, Universiteit Utrecht, 2002.Google Scholar
[30] Zwegers, S. P., Appell-Lerch sums as mock modular forms. Conference presentation, KIAS, June 26, 2008.Google Scholar