No CrossRef data available.
Published online by Cambridge University Press: 29 June 2021
Let G be a connected reductive group over a p-adic number field F. We propose and study the notions of G-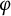 $\varphi $
-modules and G-
$\varphi $
-modules and G-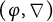 $(\varphi ,\nabla )$
-modules over the Robba ring, which are exact faithful F-linear tensor functors from the category of G-representations on finite-dimensional F-vector spaces to the categories of
$(\varphi ,\nabla )$
-modules over the Robba ring, which are exact faithful F-linear tensor functors from the category of G-representations on finite-dimensional F-vector spaces to the categories of 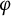 $\varphi $
-modules and
$\varphi $
-modules and 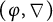 $(\varphi ,\nabla )$
-modules over the Robba ring, respectively, commuting with the respective fiber functors. We study Kedlaya’s slope filtration theorem in this context, and show that G-
$(\varphi ,\nabla )$
-modules over the Robba ring, respectively, commuting with the respective fiber functors. We study Kedlaya’s slope filtration theorem in this context, and show that G-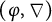 $(\varphi ,\nabla )$
-modules over the Robba ring are “G-quasi-unipotent,” which is a generalization of the p-adic local monodromy theorem proved independently by Y. André, K. S. Kedlaya, and Z. Mebkhout.
$(\varphi ,\nabla )$
-modules over the Robba ring are “G-quasi-unipotent,” which is a generalization of the p-adic local monodromy theorem proved independently by Y. André, K. S. Kedlaya, and Z. Mebkhout.
This paper is partially supported by a research grant from Shanghai Key Laboratory of PMMP 18dz2271000.