Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-23T23:22:47.269Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups with a Certain Condition on Conjugates

Published online by Cambridge University Press:  20 November 2018

Franklin Haimo
Franklin Haimo*
Affiliation:
Washington University in Saint Louis
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we shall show that if 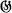is a nilpotent [5] group and if M, a positive integer, is a uniform bound on the number of conjugates that any element of 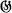may have, then there exist “large” integers n for which x → xn is a central endomorphism o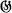f . If 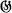is not necessarily nilpotent, if the above condition on the conjugates is retained, and if we can find a member of the lower central series [1], every element of which lies in some member of the ascending central series, then we shall show that every non-unity element of the “high” derivatives has finite order.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 4 , 1952 , pp. 369 - 372
Copyright
Copyright © Canadian Mathematical Society 1952

References

1. Baer, R., The higher commutator subgroups of a group, Bull. Amer. Math. Soc, vol. 50 (1944), 143–160.Google Scholar
2. Bruck, R. H., Contributions to the theory of loops, Trans. Amer. Math. Soc, vol. 60 (1946), 245–354.Google Scholar
3. Levi, F. W., Notes on group theory VII, J. Indian Math. Soc. (N.S.), vol. 9 (1945), 37-42 (as available in Math. Rev., vol. 8 (1947), 13).Google Scholar
4. Neumann, B. H., Groups with finite classes of conjugate elements, Proc. London Math. Soc. (3), vol. 1 (1951), 178–187.Google Scholar
5. Zassenhaus, H., Lehrbuch der Gruppentheorie (Leipzig and Berlin, 1937).Google Scholar