Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:26:32.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Green's Potentials with Prescribed Boundary Values

Published online by Cambridge University Press:  20 November 2018

Jang-Mei G. Wu
Jang-Mei G. Wu*
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let U, C denote the open unit disk and unit circumference, respectively and G(z, w) be the Green's function on U. We say v is the Green's potential of a mass distribution v on U if

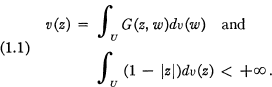
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 4 , 01 August 1977 , pp. 681 - 686
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Arsove, M. and Huber, A., On the existence of non-tangential limits of subharmonic functions, Jour. London Math. Soc. Jfl (1967), 125–132.Google Scholar
2. Helms, L. L., Introduction to potential theory (Wiley-Interscience, New York, 1969).Google Scholar
3. Littlewood, J. E., On functions subharmonic in a circle (II), Proc. London Math. Soc. (2) 28 (1928), 383–394.Google Scholar
4. Rudin, W., Boundary values of continuous analytic functions, Proc. American Math. Soc. 7 (1956), 808–811.Google Scholar
5. Tolsted, E. B., Limiting values of subharmonic functions, Proc. American Math. Soc. 1 (1950), 636–647.Google Scholar
6. Tolsted, E. B., Nontangential limits of subharmonic functions, Proc. London Math. Soc. (3) 7 (1957), 321–333.Google Scholar