Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T05:39:01.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Girsanov Transformations for Non-Symmetric Diffusions

Published online by Cambridge University Press:  20 November 2018

Chuan-Zhong Chen  and
Wei Sun
Chuan-Zhong Chen
Affiliation:
Department of Mathematics, Hainan Normal University, Haikou, 571158, China, [email protected]
Wei Sun
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montreal, H3G 1M8, Canada, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 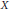$X$ be a diffusion process, which is assumed to be associated with a (non-symmetric) strongly local Dirichlet form 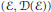$(\varepsilon ,\mathcal{D}(\varepsilon ))$ on 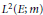${{L}^{2}}(E;m)$. For 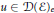$u\,\in \,\mathcal{D}{{(\varepsilon )}_{e}}$, the extended Dirichlet space, we investigate some properties of the Girsanov transformed process 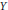$Y$ of 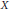$X$. First, let 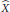$\hat{X}$ be the dual process of 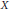$X$ and 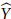$\hat{Y}$ the Girsanov transformed process of 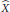$\hat{X} $. We give a necessary and sufficient condition for 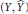$(Y,\hat{Y})$ to be in duality with respect to the measure 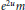${{e}^{2u}}m$. We also construct a counterexample, which shows that this condition may not be satisfied and hence 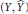$(Y,\hat{Y})$ may not be dual processes. Then we present a sufficient condition under which 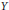$Y$ is associated with a semi-Dirichlet form. Moreover, we give an explicit representation of the semi-Dirichlet form.

Keywords

60J4531C2560J57Diffusionnon-symmetric Dirichlet formGirsanov transformationh-transformationperturbation of Dirichlet formgeneralized Feynman-Kac semigroup
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 534 - 547
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Albeverio, S. and Ma, Z. M., Perturbation of Dirichlet forms–lower semiboundedness, closablility, and form cores. J. Funct. Anal. 99(1991), no. 2, 332–356.Google Scholar
[2] Albeverio, S. and Ma, Z. M., Additive functionals, nowhere Radon and Kato class smooth measures associated with Dirichlet forms. Osaka J. Math. 29(1992), no. 2, 247–265.Google Scholar
[3] Chen, C. Z., Perturbation of Dirichlet forms and Feynman-Kac semigroups. Ph. D. Thesis, Central South University, 2004.Google Scholar
[4] Chen, C. Z., A note on perturbation of non-symmetric Dirichlet forms by signed smooth measures. Math. Acta. Sci. Ser. B Engl. Ed. 27(2007), no. 1, 219–224.Google Scholar
[5] Chen, C. Z. and Sun, W., Perturbation of non-symmetric Dirichlet forms and associated Markov processes. Acta. Math. Sci. Ser. A Chin. Ed. 21(2001), no. 2, 145–153.Google Scholar
[6] Chen, C. Z. and Sun, W., Strong continuity of generalized Feynman-Kac semigroups: necessary and sufficient conditions. J. Funct. Anal. 237(2006), no. 2, 446–465.Google Scholar
[7] Chen, Z. Q., Fitzsimmons, P. J., Takeda, M., Ying, J., and Zhang, T.-S., Absolute continuity of symmetric Markov processes. Ann. Probab. 32(2004), no. 3A, 2067–2098.Google Scholar
[8] Chen, Z. Q. and T.-S. Zhang, Girsanov and Feynman-Kac type transformations for symmetric Markov processes. Ann. Inst. H. Poincarè Probab. Statist. 38(2002), no. 4, 475–505.Google Scholar
[9] Eberle, A., Girsanov-type transfomations of local Dirichlet forms: an analytic approach. Osaka J. Math. 33(1996), no. 2, 497–531.Google Scholar
[10] Fitzsimmons, P. J., Even and odd continuous additive functionals. In: Dirichlet forms and stochastic processes, de Gruyter, Berlin, 1995, pp. 139–154.Google Scholar
[11] Fitzsimmons, P. J., Absolute continuity of symmetric diffusions. Ann. Probab. 25(1997), no. 1, 230–258.Google Scholar
[12] Fukushima, M., On absolute continuity of multi-dimensional symmetrizable diffusions. In: Functional analysis in Markov processes, Lecture Notes in Math. 923, Springer-Verlag, Berlin-New York, 1982, pp. 146–176.Google Scholar
[13] Fukushima, M., Oshima, Y., and Takeda, M., Dirichlet forms and symmetric Markov processes. de Gruyer Studies in Mathematics 19, Walter de Gruyrer, Berlin, 1994.Google Scholar
[14] Fukushima, M. and Takeda, M., A transformation of a symmetric Markov process and the Donsker-Varadhan theory. Osaka J. Math. 21(1984), no. 2, 311–326.Google Scholar
[15] Ma, Z. M. and Röckner, M., Introduction to the theory of (non-symmetric) Dirichlet forms. Springer-Verlag, Berlin, 1992.Google Scholar
[16] Oshima, Y., Lectures on Dirichlet Spaces, Universität Erlangen-Nürnberg, 1988. http://www.srik.kumamoto-u.ac.jp.Google Scholar
[17] Oshima, Y. and Takeda, M., On a transformation of symmetric Markov processes and recurrence property. In: Stochastic processes—mathematics and physics II, Lecture Notes in Math. 1250, Springer, Berlin, 1987, pp. 171–183.Google Scholar
[18] Sharpe, M. J., General theory of Markov processes. Pure and Applied Mathematics 133, Academic Press, Boston, MA, 1988.Google Scholar
[19] Wang, Y. X., Transformation of Dirichlet Form. Ph. D. Thesis, Institute of Applied Mathematices, Academia Sinica, 1994.Google Scholar