Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-02T23:37:57.406Z Has data issue: false hasContentIssue false
  • English
  • Français

The Gibbs Phenomenon for Generalized Taylor and Euler Transforms

Published online by Cambridge University Press:  20 November 2018

Robert E. Powell  and
Richard A. Shoop
Robert E. Powell
Affiliation:
Kent State University, Kent, Ohio
Richard A. Shoop
Affiliation:
Kent State University, Kent, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be a real-valued function satisfying the Dirichlet conditions in a neighborhood of x = x0, at which point f has a jump discontinuity. If {Sn(x)} is the sequence of partial sums of the Fourier series of f at x, then ﹛Sn(x)﹜ cannot converge uniformly at x — x0. Moreover, for any number 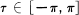, there exists a sequence ﹛tn﹜, where tn → x0 and

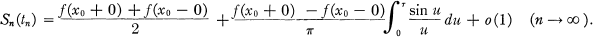
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 2 , 01 April 1975 , pp. 384 - 395
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Cramer, H., Etudes sur la sommation des series de Fourier, Arkiv for Mathematik, Astronomi, och Fysik, 13, No. 20 (1919), 1–21.Google Scholar
2. Gronwall, T. H., Zur Gibbschen Erscheinung, Ann. of Math. 31 (1930), 233–240.Google Scholar
3. Kuttner, B., On the Gibbs phenomenon for Riesz means, J. London Math. Soc. 19 (1944), 153–161.Google Scholar
4. Lorch, L., The Gibbs phenomenon for Borel means, Proc. Amer. Math. Soc. 8 (1957), 81–84.Google Scholar
5. Miracle, C. L., The Gibbs phenomenon for Taylor means and for [F, dn] means, Can. J. Math. 12 (1960), 660–673.Google Scholar
6. Powell, R. E., Theƒ(rn) summability transform, J. Analyse Math. 20 (1967), 289–304,Google Scholar
7. Powell, R. E., TheL(r, t) summability transform, Can. J. Math. 18 (1966), 1251–1260.Google Scholar
8. Sledd, W. T., The Gibbs phenomenon and Lebesgue constants for regular Sonnenschein matrices, Can. J. Math. U (1962), 723–728.Google Scholar
9. Szâsz, O., On the Gibbs phenomenon for Euler means, Acta Sci. Math. (Szeged) 12 (1950), 107–111.Google Scholar
10. Szâsz, O., Gibbs phenomenon for Hausdorff means, Trans. Amer. Math. Soc. 69 (1950), 440–456.Google Scholar
11. Wood, B., A generalized Euler summability transform, Math. Z. 105 (1968), 36–48.Google Scholar