Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-03T20:32:37.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry on the Unit Ball of a Complex Hilbert Space

Published online by Cambridge University Press:  20 November 2018

Kyong T. Hahn
Kyong T. Hahn*
Affiliation:
The Pennsylvania State University, University Park, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Furnishing the open unit ball of a complex Hilbert space with the Carathéodory-differential metric, we construct a model 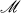which plays a similar role as that of the Poincaré model for the hyperbolic geometry.

In this note we study the question whether or not through a point in the model 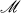not lying on a given line there exists a unique perpendicular, and give a necessary and sufficient condition for the existence of a unique perpendicular. This enables us to divide a triangle into two right triangles. Many trigonometric identities in a general triangle are easy consequences of various identities which hold on a right triangle.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 1 , 01 February 1978 , pp. 22 - 31
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Earle, C. J. and Hamilton, R. S., A fixed point theorem for holomorphic mappings, Global Analysis, Proc. of Symposium in Pure Math. XVI (Amer. Math. Soc, Providence, R.I., 1965).Google Scholar
2. Hahn, K. T., The non-euclidean Pythagorean theorem with respect to the Bergman metric, Duke Math. J. 33 (1966), 523–534.Google Scholar
3. Hahn, K. T., Trigonometry in a hyperbolic space, Duke Math. J. 35 (1968), 739–746.Google Scholar
4. Hahn, K. T., Trigonometry on the unit ball of a complex Hilbert space, Bull. Amer. Math. Soc. 81 (1975).Google Scholar
5. Harris, L. A., Schwarz's lemma and the maximum principle in infinite dimensional spaces, Thesis, Cornell University, Ithaca, N.Y., 1969.Google Scholar
6. Harris, L. A., Bounded symmetric homogeneous domains in infinite dimensional spaces, Lecture Notes in Math. 364, Proceedings on Infinite Dimensional Holomorphy (Springer-Verlag, Berlin, 1974), 13–40.Google Scholar
7. Renaud, A., Quelques propriétés des applications analytiques d'une boule de dimension infine dans une autre, Bull. Sci. Math. 97 (1973), 129–159.Google Scholar
8. Reiffen, H. J., Die differential geometrischen Eigenschaften der invarianten Distanzfunktion von Carathéodory, Schrift Math. Inst. Univ. Munster 26 (1963).Google Scholar