Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T09:29:30.485Z Has data issue: false hasContentIssue false
  • English
  • Français

The Geometry of the Weak Lefschetz Property and Level Sets of Points

Published online by Cambridge University Press:  20 November 2018

Juan C. Migliore
Juan C. Migliore*
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper, F. Zanello showed that level Artinian algebras in 3 variables can fail to have the Weak Lefschetz Property 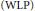$(\text{WLP})$, and can even fail to have unimodal Hilbert function. We show that the same is true for the Artinian reduction of reduced, level sets of points in projective 3-space. Our main goal is to begin an understanding of how the geometry of a set of points can prevent its Artinian reduction from having $\text{WLP}$, which in itself is a very algebraic notion. More precisely, we produce level sets of points whose Artinian reductions have socle types 3 and 4 and arbitrary socle degree ≥ 12 (in the worst case), but fail to have $\text{WLP}$. We also produce a level set of points whose Artinian reduction fails to have unimodal Hilbert function; our example is based on Zanello's example. Finally, we show that a level set of points can have Artinian reduction that has $\text{WLP}$ but fails to have the Strong Lefschetz Property. While our constructions are all based on basic double $G$-linkage, the implementations use very different methods.

Keywords

13D4013D0214C2013C4013C1314M05Weak Lefschetz PropertyStrong Lefschetz Propertybasic double G-linkagelevelarithmetically Gorensteinarithmetically Cohen–Macaulaysocle typesocle degreeArtinian reduction
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 2 , 01 April 2008 , pp. 391 - 411
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Anick, D., Thin algebras of embedding dimension three. J. Algebra 100(1986), no. 1, 235–259.Google Scholar
[2] Bernstein, D. and Iarrobino, A., A nonunimodal graded Gorenstein Artin algebra in codimension five. Comm. Alg. 20(1992), no. 8, 2323–2336.Google Scholar
[3] Boij, M., Graded Gorenstein Artin algebras whose Hilbert functions have a large number of valleys. Comm. Algebra 23(1995), no. 1, 97–103.Google Scholar
[4] Boij, M. and Laksov, D., Nonunimodality of graded Gorenstein Artin algebras. Proc. Amer.Math. Soc. 120(1994), no. 4, 1083–1092.Google Scholar
[5] Boij, M. and Zanello, F., Level algebras with bad properties. Proc. Amer.Math. Soc. 135(2007), no. 9, 2713–2722.Google Scholar
[6] CoCoA: A System for Doing Computations in Commutative Algebra. Available at http://cocoa.dima.unige.it.Google Scholar
[7] Davis, E., Geramita, A. V., and Orecchia, F., Gorenstein algebras and the Cayley-Bacharach theorem. Proc. Amer. Math. Soc. 93(1985), no. 4, 593–597.Google Scholar
[8] Eisenbud, D. and Popescu, S., Gale duality and free resolutions of ideals of points. Invent.Math. 136(1999), no. 2, 419–449.Google Scholar
[9] Geramita, A. V., Gregory, D., and Roberts, L., Monomial ideals and points in projective space. J. Pure Appl. Algebra 40(1986), no. 1, 33–62.Google Scholar
[10] Geramita, A. V., Maroscia, P., and Roberts, L., The Hilbert function of a reduced k-algebra. J. London Math. Soc. 28(1983), no. 3, 443–452.Google Scholar
[11] Geramita, A. V., Harima, T., Migliore, J., and Shin, Y. S., The Hilbert function of a level algebra, Mem. Amer. Math. Soc. 186(2007), no. 872.Google Scholar
[12] Geramita, A. V. and Migliore, J., Reduced Gorenstein codimension three subschemes of projective space. Proc. Amer.Math. Soc. 125(1997), no. 4, 943–950.Google Scholar
[13] Harima, T., Migliore, J., Nagel, U., and Watanabe, J., The Weak and Strong Lefschetz Properties for Artinian K-algebras. J. Algebra 262(2003), no. 1, 99–126.Google Scholar
[14] Hartshorne, R., Connectedness of the Hilbert scheme. Inst. Hautes Études Sci. Publ. Math. 29(1966), 5–48.Google Scholar
[15] Iarrobino, A. and Kanev, V., Power Sums, Gorenstein Algebras, and Determinantal Loci. Lecture Notes in Mathematics 1721, Springer-Verlag, Berlin, 1999.Google Scholar
[16] Ikeda, H., Results on Dilworth and Rees numbes of Artinian local rings. Japan. J. Math. 22(1996), no. 1, 147–158.Google Scholar
[17] Kleppe, J., Migliore, J., Miró-Roig, R. M., Nagel, U., and Peterson, C., Gorenstein liaison, complete intersection liaison invariants and unobstructedness. Mem. Amer. Math. Soc. 154(2001), no. 732.Google Scholar
[18] Lorenzini, A., The minimal resolution conjecture. J. Algebra 156(1993), no. 1, 5–35.Google Scholar
[19] Macaulay, F. S., Some properties of enumeration in the theory of modular systems. Proc. Lond. Math. Soc. 26(1927) 531–555.Google Scholar
[20] Migliore, J., Submodules of the deficiency module. J. Lond. Math. Soc. 48(1993), no. 3, 396–414.Google Scholar
[21] Migliore, J., Introduction to Liaison Theory and Deficiency Modules. Progress in Mathematics 165, Birkhäuser Boston, Boston,MA, 1998.Google Scholar
[22] Migliore, J., Families of reduced, zero-dimensional schemes. Collect. Math 57(2006), no. 2, 173–192.Google Scholar
[23] Migliore, J. and Nagel, U., Lifting monomial ideals. Comm. Algebra 28(2000), no. 12, 5679–5701.Google Scholar
[24] Migliore, J. and Nagel, U., Reduced arithmetically Gorenstein schemes and simplicial polytopes with maximal Betti numbers. Adv. Math. 180(2003), no. 1, 1–63.Google Scholar
[25] Stanley, R., Hilbert Functions of graded algebras. Adv. Math. 28(1978), no. 1, 57–83.Google Scholar
[26] Zanello, F., A non-unimodal codimension 3 level h-vector. J. Algebra 305(2006), no. 2, 949–956.Google Scholar