Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T19:24:27.785Z Has data issue: false hasContentIssue false
  • English
  • Français

The Geometry of GF(q3)

Published online by Cambridge University Press:  20 November 2018

F. A. Sherk
F. A. Sherk*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Inversive geometry involves as basic entities points and circles [2, p. 83; 4, p. 252]. The best known examples of inversive planes (the Miquelian planes) are constructed from a field K which is a quadratic extension of some other field F. Thus the complex numbers yield the Real Inversive Plane, while the Galois field GF(q2)(q = pe, p prime) yields the Miquelian inversive plane M(q) [2, chapter 9; 4, p. 257]. The purpose of this paper is to describe an analogous geometry of M(q) which derives from GF(q3), the cubic extension of GF(q).

The resulting space, 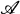is three-dimensional, involving a class 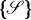of surfaces which include planes, some quadric surfaces, and some cubic surfaces. We explore these surfaces, giving particular attention to the number of points they contain, and their intersections with lines and planes of the space .

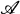Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 3 , 01 June 1986 , pp. 672 - 696
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Bruck, R. H., Circle geometry in higher dimensions II, Geom. Ded. 2 (1973), 133–188.Google Scholar
2. Coxeter, H. S. M., Introduction to geometry (Wiley, New York, 1969).Google Scholar
3. Coxeter, H. S. M., Projective geometry (Blaisdell, Waltham, Mass., 1964).Google Scholar
4. Dembowski, P., Finite geometries (Springer-Verlag, Berlin, 1968).CrossRefGoogle Scholar
5. Hall, M. Jr., Cyclic projective planes, Duke Math. J. 14 (1947), 1079–1090.Google Scholar
6. Hirschfeld, J. W. P., Projective geometries over finite fields (Clarendon Press, Oxford, 1979).Google Scholar
7. Jungnickel, D. and Vedder, K., On the geometry of planar difference sets, Europ. J. Combinatorics 5 (1984), 143–148.Google Scholar
8. Singer, J., A theorem in finite projective geometry and some applications to number theory, Trans. Amer. Math. Soc. 43 (1938), 377–385.Google Scholar