Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T23:18:32.693Z Has data issue: false hasContentIssue false
  • English
  • Français

A Geometrical Approach to the Second-Order Linear Differential Equation

Published online by Cambridge University Press:  20 November 2018

C. M. Petty  and
J. E. Barry
C. M. Petty
Affiliation:
Lockheed Missiles and Space Division, Palo Alto
J. E. Barry
Affiliation:
Hughes Aircraft Co., Culver City
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper various concepts intrinsically defined by the differential equation

1.1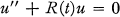

are interpreted geometrically by concepts analogous to those in the Minkowski plane. This is carried out in § 2. The point of such a development is that one may apply the techniques or transfer known results in the theory of curves (in particular, convex curves) to (1.1), thereby gaining an additional tool in the investigation of this equation. For an application of a result obtained in this way, namely (3.12), see (4).

Throughout this paper, R(t) is a real-valued, continuous function of t on the real line (— ∞ < t < + ∞) and only the real solutions of (1.1) are considered.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 349 - 358
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Busemann, H., The foundation of Minkowski geometry, Comm. Math. Helv., 24 (1950), 156–187.Google Scholar
2. Busemann, H., The isoperimetric problem in the Minkowski plane, Amer. J. Math., 69 (1947), 863–871.Google Scholar
3. Finsler, P., Ueber eine Verallgemeinerung des Satzes von Meusnier, Vierteljschr. Naturforsch. Ges., Zurich, 85 (1940), 155–164.Google Scholar
4. Green, L. W., Proof of Blaschke's sphere conjecture, Bull. Amer. Math. Soc, 67 (1961), 156–158.Google Scholar
5. Mahler, K., Ein Uebertragungsprinzipfur konvexe Kôrper, Casopis Pëst. Mat. Fys., 55 (1939), 93–102.Google Scholar
6. Petty, C M., On the geometry of the Minkowski plane, Rivista di Matematica della Universita di Parma, 6 (1955), 269–292.Google Scholar
7. Santalo, L. A., Un invariante afin para los cuerpos convexos del espacio de n-dimensiones, Portugaliae Math., 8 (1949), 155–161.Google Scholar