No CrossRef data available.
Article contents
Generalized Resolvent Equations and Unsymmetric Dirichlet Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
Let (X, 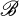 , μ) and (X,
, μ) and (X, 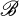 , μ′) be measure spaces with the measures μ and μ′ totally finite. Suppose {Uλ: λ > 0} is a family of positive (i.e., ϕ ≧ 0 ⇒ Uλϕ ≧ 0) continuous linear operators from L2(X, dμ′) to L2(X,dμ) with the following additional properties: if ϕ ≧ 0 then Uλϕ is non-decreasing as λ increases, while λ−1Uλϕ is nonincreasing.
, μ′) be measure spaces with the measures μ and μ′ totally finite. Suppose {Uλ: λ > 0} is a family of positive (i.e., ϕ ≧ 0 ⇒ Uλϕ ≧ 0) continuous linear operators from L2(X, dμ′) to L2(X,dμ) with the following additional properties: if ϕ ≧ 0 then Uλϕ is non-decreasing as λ increases, while λ−1Uλϕ is nonincreasing.
A family {Mλ:λ > 0} of continuous linear operators from L2(X, dμ) to L2(X, dμ′) satisfies the “generalized resolvent equation” relative to {Uλ} if
(0.1)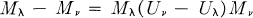
for positive λ and v. If Uλ = λI, then (0.1) is just the well-known resolvent equation. The family {Mλ} is called submarkov if Mλ is a positive operator and
(0.2)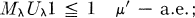
it is conservative if
(0.3)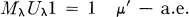
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981


