Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T06:02:31.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Polynomials and Mild Mixing

Published online by Cambridge University Press:  20 November 2018

Randall McCutcheon  and
Anthony Quas
Randall McCutcheon
Affiliation:
Department of Mathematical Sciences, University ofMemphis, Memphis, TN, USA, [email protected]
Anthony Quas
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, BC, Canada, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An unsettled conjecture of V. Bergelson and I. Håland proposes that if 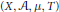$(X,\,\mathcal{A},\,\mu ,\,T)$ is an invertible weak mixing measure preserving system, where 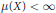$\mu (X)<\infty $, and if 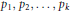${{p}_{1}},{{p}_{2}},...,{{p}_{k}}$ are generalized polynomials (functions built out of regular polynomials via iterated use of the greatest integer or floor function) having the property that no 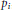${{p}_{i}}$, nor any 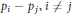${{p}_{i}}-{{p}_{j,}}i\ne j$, is constant on a set of positive density, then for any measurable sets 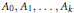${{A}_{0}},{{A}_{1}},...,{{A}_{K}}$, there exists a zero-density set 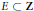$E\subset Z$ such that

1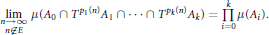

$$\underset{n\notin E}{\mathop{\underset{n\to \infty }{\mathop{\lim }}\,}}\,\mu ({{A}_{0}}\cap {{T}^{p1(n)}}{{A}_{1}}\cap \ldots \cap {{T}^{pk(n)}}{{A}_{k}})=\prod\limits_{i=0}^{k}{\mu ({{A}_{i}}).}$$

We formulate and prove a faithful version of this conjecture for mildly mixing systems and partially characterize, in the degree two case, the set of families 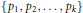$\left\{ {{p}_{1}},{{p}_{2}},\,.\,.\,.\,,\,{{p}_{k}} \right\}$ satisfying the hypotheses of this theorem.

Keywords

37A2528D05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 656 - 673
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bergelson, V., Weakly mixing PET. Ergodic Theory Dynam. System. 7(1987), no. 3, :337–349.Google Scholar
[2] Bergelson, V., Furstenberg, H., and McCutcheon, R., IP-sets and polynomial recurrence. Ergodic Theory Dynam. System. 16(1996), no. 5, 963–974.Google Scholar
[3] Bergelson, V., H°aland-Knutson, I., and McCutcheon, R., IP-systems, generalized polynomials and recurrence. Ergodic Theory Dynam. System. 26(2006), 999–1019.Google Scholar
[4] Bergelson, V. and McCutcheon, R., An ergodic IP polynomial Szemerèdi theorem. Mem. Amer. Math. Soc. 146(2000), no. 695.Google Scholar
[5] Franzikinakis, N. and Kra, B., Polynomial averages converge to the product of integrals. Israel J. Math. 148(2005), 267–276.Google Scholar
[6] Furstenberg, H., Ergodic behavior of diagonal measures and a theorem of Szemerèdi on arithmetic progressions. J. Analyse Math. 31(1977), 204–256.Google Scholar
[7] Furstenberg, H., Recurrence in ergodic theory and combinatorial number theory. M. B. Porter Lectures, Princeton University Press, Princeton, NJ, 1981.Google Scholar
[8] Furstenberg, H. and Katznelson, Y., An ergodic Szemerèdi theorem for IP-systems and combinatorial theory. J. Analyse Math. 45(1985), 117–168.Google Scholar
[9] Furstenberg, H. and Weiss, B., The finite multipliers of infinite ergodic transformations. In: The structure of attractors in dynamical systems, Lecture Notes in Mathematics 668, Springer, Berlin, 1978, pp. 61–85.Google Scholar
[10] Hindman, N., Finite sums from sequences within cells of a partition of N. J. Combinatorial Theory Ser. A 17(1974), 1–11.Google Scholar
[11] McCutcheon, R., FVIP systems and multiple recurrence. Israel J. Math. 146(2005), 157–188.Google Scholar
[12] McCutcheon, R., An infinitary polynomial van derWaerden theorem. J. Combin. Theory Ser.. 86(1999), no. 2, 214–231.Google Scholar
[13] Milliken, K., Ramsey's theorem with sums or unions. J. Combinatorial Theory Ser.. 18(1975), 276–290.Google Scholar
[14] Taylor, A. D., A canonical partition relation for finite subsets of ω. J. Combinatorial Theory Ser. A 21(1976), no. 2, 137–146.Google Scholar