Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T22:56:28.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Bloch Mappings in Complex Hilbert Space

Published online by Cambridge University Press:  20 November 2018

Fletcher D. Wicker
Fletcher D. Wicker*
Affiliation:
2806 Brant Street, San Diego, California
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

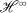Anderson, Clunie and Pommerenke defined and studied the family of Bloch functions on the unit disc (see [1]). This family strictly contains the space of bounded analytic functions. However, all Bloch functions are normal and therefore enjoy the “nice” properties of normal functions. The importance of the Bloch function concept is the combination of their richness as a family and their “nice” behavior.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 2 , 01 April 1977 , pp. 299 - 306
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Anderson, J. M., Clunie, J., and Pommerenke, Ch., On Bloch functions and normal functions, J. Reine Angew. Math. 270 (1974), 12–37.Google Scholar
2. Earle, Clifford J. and Hamilton, Richard S., A fixed point theorem for holomorphic mappings, Global Analysis, Proc. of Symposium in Pure Math. XVI, (Amer. Math. Soc. Providence, R.I., 196.5).Google Scholar
3. Hahn, Kyong T.. Hyperbolic geometry on the unit ball of a complex Hilbert space, to appear.Google Scholar
4. Holomorphic mappings of the hyperbolic space into the complex Euclidean space and the Bloch theorem, Can. J. Math. 27 (1975), 446–4, 58.Google Scholar
5. Hille, Einar, and Phillips, Ralph S., Functional analysis and semigroups, Amer. Math. Soc. Colloquium Publications, Vol. 81 (Amer. Math. Soc, Providence, R.I. 1957).Google Scholar
6. Nachbin, Leopoldo, Topology on spaces of holomorphic mappings, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band Iff (Springer Verlag, New York, 1969).Google Scholar