Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T22:51:19.100Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalized Averaging Operator

Published online by Cambridge University Press:  20 November 2018

D. B. Sumner
D. B. Sumner*
Affiliation:
Hamilton College, McMaster University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. The averaging operator 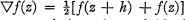has an extensive literature, the most detailed account being that of Nörlund

(4). In discussing solutions of the functional relation

1.1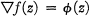

he defines a “principal solution” (4, p. 41) by means of a summability process, and later, working in terms of complex numbers, he obtains (4, p. 70) a principal solution of (1.1) by means of a contour integral. He distinguishes his principal solution from other solutions, by showing that it is continuous at h = 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 8 , 1956 , pp. 437 - 446
Copyright
Copyright © Canadian Mathematical Society 1956

References

1. Barnes, E. W., A new development of the theory of the hyper geometric functions, Proc. London Math. Soc. (2), 6 (1908), 141–177.Google Scholar
2. Jordan, C., Calculus of Finite Differences (New York, 1947).Google Scholar
3. Milne-Thomson, L., Two classes of generalized polynomials, Proc. London Math. Soc. (2), 85 (1933), 514–522.Google Scholar
4. Nörlund, N. E., Vorlesungen über Differenzenrechnung (Berlin, 1924).Google Scholar
5. Tirchmarsh, E. C., The Theory of Functions (2nd. ed., Oxford 1939).Google Scholar