Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T05:33:00.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalization of the Hausdorff Moment Problem

Published online by Cambridge University Press:  20 November 2018

David Borwein  and
Amnon Jakimovski
David Borwein
Affiliation:
The University of Western Ontario, London, Ontario
Amnon Jakimovski
Affiliation:
Tel-Aviv University, Tel-Avivy Israel
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose throughout that {kn} is a sequence of positive integers, that

that k0 = 1 if l0 = 1, and that {un(r)}; (r = 0, 1, …, kn – 1, n = 0, 1, …) is a sequence of real numbers. We shall be concerned with the problem of establishing necessary and sufficient conditions for there to be a function a satisfying

(1)

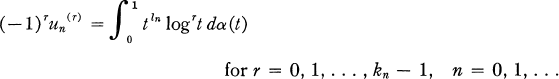
and certain additional conditions. The case l0 = 0, kn = 1 for n = 0, 1, … of the problem is the version of the classical moment problem considered originally by Hausdorff [5], [6], [7]; the above formulation will emerge as a natural generalization thereof.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 946 - 960
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Berman, D. L., Application of interpolatory polynomial operators to solve the moment problem, Urkain Math. Z. 14 (1963), 184–190.Google Scholar
2. Borwein, D., The Hausdorff moment problem, Can. Math. Bull. 21 (1978), 257–265; Corrections 22 (1979), 128.Google Scholar
3. Davis, P. J., Interpolation and approximation (Blaisdell, New York, 1965).Google Scholar
4. Endl, K., On systems of linear inequalities in infinitely many variables and generalized Hausdorff means, Math. Z. 82 (1963), 1–7.Google Scholar
5. Hausdorff, F., Summationsmethoden und Moment﹜olgen I, Math. Z. 9 (1921), 74–109.Google Scholar
6. Hausdorff, F., Summationsmethoden und Momentfolgen II, Math. Z. 9 (1921), 280–299.Google Scholar
7. Hausdorff, F., Momentprobleme fur ein eindliches Interval, Math. Z. 16 (1923), 220–248.Google Scholar
8. Krasnosel'skii, M. A. and Rutickk, Ya. B., Convex functions and Orlicz spaces (P. Noordhoff, Groningen, 1961).Google Scholar
9. Leviatan, D., A generalized moment problem, Israel J. Math. 5 (1967), 97–103.Google Scholar
10. Leviatan, D., Some moment problems in a finite interval, Can. J. Math. 20 (1968), 960–966.Google Scholar
11. Lorentz, G. G., Bernstein polynomials (University of Toronto Press, Toronto, 1953).Google Scholar
12. Medvedev, U. T., Generalization of a theorem of F. Riesz, Uspeshi, Mat. Nauk 8 (1953), 115–118.Google Scholar
13. Schoenberg, I. J., On finite rowed systems of linear inequalities in infinitely many variables, Trans. A.M.S. 34 (1932), 594–619.Google Scholar
14. Widder, D. V., The Laplace transform (Princeton, 1946).Google Scholar
15. Zygmund, A., Trigonometric series I, 2nd edition (Cambridge University Press, Cambridge, 1959).Google Scholar