Article contents
A Generalization of Commutative and Alternative Rings II
Published online by Cambridge University Press: 20 November 2018
Extract
We shall call a linear function on the elements of a ring R skew-symmetric if it vanishes whenever at least two of the variables are equal. Here we shall study rings R of characteristic not 2 which satisfy the following two identities:
1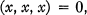
(2)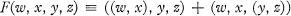 is skew-symmetric.
is skew-symmetric.
Both of these identities hold in alternative rings. The fact that F(w, x, y, z) is skew-symmetric in alternative rings is an important tool in the study of such rings. It is also obvious that both identities hold in commutative rings. But unlike other recent generalizations of commutative and alternative rings it turns out that there exist simple, finite dimensional algebras of degree two which are neither alternative nor commutative and satisfy (1) and (2).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
- 1
- Cited by


