Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T15:19:02.526Z Has data issue: false hasContentIssue false
  • English
  • Français

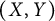General Toeplitz kernels and $(X,Y)$-invariance

Part of: General theory of linear operators Special classes of linear operators Spaces and algebras of analytic functions

Published online by Cambridge University Press:  27 March 2023

M. Cristina Câmara ,
Kamila Kliś-Garlicka Open the ORCID record for Kamila Kliś-Garlicka [Opens in a new window]  and
Marek Ptak Open the ORCID record for Marek Ptak [Opens in a new window]
M. Cristina Câmara
Affiliation:
Center for Mathematical Analysis, Geometry and Dynamical Systems, Mathematics Department, Instituto Superior Técnico, Universidade de Lisboa, Avenida Rovisco Pais, 1049-001 Lisboa, Portugal e-mail: [email protected]
Kamila Kliś-Garlicka*
Affiliation:
Department of Applied Mathematics, University of Agriculture, Ulica Balicka 253c, 30-198 Kraków, Poland e-mail: [email protected]
Marek Ptak
Affiliation:
Department of Applied Mathematics, University of Agriculture, Ulica Balicka 253c, 30-198 Kraków, Poland e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the near invariance of model spaces for the backward shift, we introduce a general notion of 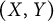$(X,Y)$-invariant operators. The relations between this class of operators and the near invariance properties of their kernels are studied. Those lead to orthogonal decompositions for the kernels, which generalize well-known orthogonal decompositions of model spaces. Necessary and sufficient conditions for those kernels to be nearly X-invariant are established. This general approach can be applied to a wide class of operators defined as compressions of multiplication operators, in particular to Toeplitz operators and truncated Toeplitz operators, to study the invariance properties of their kernels (general Toeplitz kernels).

Keywords

Model spacetruncated Toeplitz operatorshift invariantToeplitz kernelnearly invariantinvariant with defect

MSC classification

Primary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Secondary: 47A15: Invariant subspaces 47B32: Operators in reproducing-kernel Hilbert spaces (including de Branges, de Branges-Rovnyak, and other structured spaces) 30H10: Hardy spaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 2 , April 2024 , pp. 680 - 706
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The work of the first author was partially supported by FCT/Portugal through projects UIDB/04459/2020 and UIDP/04459/2020. The research of the second and third authors was financed by the Ministry of Higher Education and Science of the Republic of Poland.

References

Böttcher, A. and Speck, F.-O., On the symmetrization of general Wiener–Hopf operators . J. Operator Theory 76(2016), no. 2, 335–349. https://doi.org/10.7900/jot.2015nov21.2112 CrossRefGoogle Scholar
Brown, A. and Halmos, P., Algebraic properties of Toeplitz operators . J. Reine Angew. Math. 213(1964), 89–102. https://doi.org/10.1007/978-1-4613-8208-9_19 Google Scholar
Câmara, M. C., Jurasik, J., Kliś-Garlicka, K., and Ptak, M., Characterizations of asymmetric truncated Toeplitz operators . Banach J. Math. Anal. 11(2017), no. 4, 899–922. https://doi.org/10.1215/17358787-2017-0029 CrossRefGoogle Scholar
Câmara, M. C., Kliś-Garlicka, K., Łanucha, B., and Ptak, M., Cojugations in ${L}^2$ and their invariants. Anal. Math. Phys. 10(2020), 22. https://doi.org/10.1007/s13324-020-00364-5 CrossRefGoogle Scholar
Câmara, M. C., Malheiro, M. T., and Partington, J. R., Kernels of unbounded Toeplitz operators and factorization of symbols . Results Math. 76(2021), 10. https://doi.org/10.1007/s00025-020-01323-z CrossRefGoogle Scholar
Câmara, M. C., O’Loughlin, R., and Partington, J. R., Dual-band general Toeplitz operators . Mediterr. J. Math. 19(2022), 175. https://doi.org/10.1007/s00009-022-02087-2 CrossRefGoogle Scholar
Câmara, M. C. and Partington, J. R., Near invariance and kernels of Toeplitz operators . J. Anal. Math. 124(2014), 235–260. https://doi.org/10.1007/s11854-014-0031-8 CrossRefGoogle Scholar
Câmara, M. C. and Partington, J. R., Finite-dimensional Toeplitz kernels and nearly–invariant subspaces . J. Operator Theory 75(2016), 75–90. https://doi.org/10.7900/jot.2014oct29.2067 CrossRefGoogle Scholar
Câmara, M. C. and Partington, J. R., Spectral properties of truncated Toeplitz operators by equivalence after extension . J. Math. Anal. Appl. 433(2016), 762–784. https://doi.org/10.1016/j.jmaa.2015.08.019 CrossRefGoogle Scholar
Câmara, M. C. and Partington, J. R., Asymmetric truncated Toeplitz operators and Toeplitz operators with matrix symbol . J. Operator Theory 77(2017), 455–479. https://doi.org/10.7900/jot.2016apr27.2108 CrossRefGoogle Scholar
Chalendar, I., Gallardo-Gutiérrez, E. A., and Partington, J. R., A Beurling theorem for almost-invariant subspaces of the shift operator . J. Operator Theory 83(2020), no. 2, 321–331. https://doi.org/10.7900/jot.2018sep25.2231 CrossRefGoogle Scholar
Chattopadhyay, A. and Das, S., Study of nearly invariant subspaces with finite defect in Hilbert spaces . Proc. Math. Sci. 132(2022), 10. https://doi.org/10.1007/s12044-022-00654-x CrossRefGoogle Scholar
Devinatz, A. and Shinbrot, M., General Wiener–Hopf operators , Trans. Amer. Math. Soc. 145(1969), 467–494. https://doi.org/10.1090/s0002-9947-1969-0251573-0 CrossRefGoogle Scholar
Dymek, P., Płaneta, A., and Ptak, M., Conjugations preserving Toeplitz kernels . Integral Equations Operator Theory 94(2022), 39. https://doi.org/10.1007/s00020-022-02714-3 CrossRefGoogle Scholar
Garcia, S. and Ross, W. T., Model spaces: A survey . In: Invariant subspaces of the shift operator, Contemporary Mathematics, 638, American Mathematical Society, Providence, RI, 2015, pp. 197–245. https://doi.org/10.1090/conm/638/12811 CrossRefGoogle Scholar
Garcia, S. R. and Putinar, M., Complex symmetric operators and applications . Trans. Amer. Math. Soc. 358(2006), 1285–1315. https://doi.org/10.1090/s0002-9947-05-03742-6 CrossRefGoogle Scholar
Gu, C., Łanucha, B., and Michalska, M., Characterizations of asymmetric truncated Toeplitz and Hankel operators . Complex Anal. Oper. Theory 13(2019), 673–684. https://doi.org/10.1007/s11785-018-0783-8 CrossRefGoogle Scholar
Hartmann, A. and Ross, W. T., Truncated Toeplitz operators and boundary values in nearly invariant subspaces . Complex Anal. Oper. Theory 7(2013), no. 1, 261–273. https://doi.org/10.1007/s11785-011-0151-4 CrossRefGoogle Scholar
Hayashi, E., The kernel of a Toeplitz operator . Integral Equations Operator Theory 9(1986), 588–591. https://doi.org/10.1007/bf01204630 CrossRefGoogle Scholar
Hitt, D., Invariant subspaces of ${H}^2$ of an annulus. Pacific J. Math. 134(1988), 101–120. https://doi.org/10.2140/pjm.1988.134.101 CrossRefGoogle Scholar
Larson, D., Annihilators of operator algebras . Oper. Theory 6(1982), 119–130. https://doi.org/10.1007/978-3-0348-5445-0_10 Google Scholar
Liang, Y. and Partington, J. R., Representing kernels of perturbations of Toeplitz operators by backward shift-invariant subspaces . Integral Equations Operator Theory 92(2020), 35. https://doi.org/10.1007/s00020-020-02592-7 CrossRefGoogle Scholar
Makarov, N. and Poltoratski, A., Meromorphic inner functions, Toeplitz kernels and the uncertainty principle . In: Perspectives in analysis, Springer, Berlin–Heidelberg, 2005, pp. 185–252. https://doi.org/10.1007/3-540-30434-7_10 CrossRefGoogle Scholar
Meise, R. and Vogt, D., Introduction to functional analysis, Oxford Graduate Texts in Mathematics, Clarendon Press, Oxford, 1997.CrossRefGoogle Scholar
Mikhlin, S. G. Prössdorf, S., Singular integral operators, Springer-Verlag, Berlin, 1986, translated from the German by Albrecht Böttcher and Reinhard Lehmann. https://doi.org/10.1007/978-3-642-61631-0 CrossRefGoogle Scholar
Nikolski, N. K., Operators, functions, and systems: An easy Reading. Volume 1. Hardy, Hankel, and Toeplitz, American Mathematical Society, Providence, RI, 2002. https://doi.org/10.1090/surv/093 Google Scholar
O’Loughlin, R., Nearly invariant subspaces with applications to truncated Toeplitz operators . Complex Anal. Oper. Theory 14(2020), 86. https://doi.org/10.1007/s11785-020-01049-4 CrossRefGoogle Scholar
Sarason, D., Nearly invariant subspaces of the backward shift . In: Contributions to operator theory and its applications (Mesa, AZ, 1987), Operator Theory: Advances and Applications, 35, Birkhäuser, Basel, 1988, pp. 481–493.CrossRefGoogle Scholar
Sarason, D., Kernels of Toeplitz operators . Oper. Theory Adv. Appl. 71(1994), 153–164.Google Scholar
Sarason, D., Algebraic properties of truncated Toeplitz operators . Oper. Matrices 1(2007), 491–526.CrossRefGoogle Scholar
Speck, F.-O., General Wiener–Hopf factorization methods, Pitman, London, 1985.Google Scholar
Weisstein, E. W., Shift-invariant operator, MathWorld—A Wolfram Web Resource. https://mathworld.wolfram.com/Shift-InvariantOperator.html Google Scholar