Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tiwari, R
and
Pant, D N
1972.
Nonexistence of isolated charged monopoles in unified field theories.
Journal of Physics A: General Physics,
Vol. 5,
Issue. 3,
p.
394.
Pant, D. N.
1975.
Spherically symmetric rigorous solutions in Bonnor’s unified field theory.
Il Nuovo Cimento B Series 11,
Vol. 25,
Issue. 1,
p.
175.
Moffat, J. W.
1979.
New theory of gravitation.
Physical Review D,
Vol. 19,
Issue. 12,
p.
3554.
Klotz, A. H.
1979.
Cosmology without a cosmological principle.
Lettere Al Nuovo Cimento Series 2,
Vol. 25,
Issue. 6,
p.
190.
McInnes, B T
1980.
An identification of the metric tensor of the non-symmetric unified field theory.
Journal of Physics A: Mathematical and General,
Vol. 13,
Issue. 12,
p.
3657.
Klotz, A. H.
and
Gregory, L. J.
1981.
The nonsymmetric unified field theory.
General Relativity and Gravitation,
Vol. 13,
Issue. 2,
p.
155.
Johnson, Coates R.
1981.
Charged particles, magnetic monopoles, and topology in Einstein's unified field theory.
Physical Review D,
Vol. 24,
Issue. 2,
p.
327.
Kalinowski, M. W.
and
Kunstatter, G.
1984.
Spherically symmetric solution in the nonsymmetric Kaluza–Klein theory.
Journal of Mathematical Physics,
Vol. 25,
Issue. 1,
p.
117.
Johnson, Coates R.
1985.
Test-particle motion in Einstein’s unified field theory. I. General theory and application to neutral test particles.
Physical Review D,
Vol. 31,
Issue. 6,
p.
1236.
Mann, R. B.
1985.
Exact solutions of an algebraically extended Kaluza–Klein theory.
Journal of Mathematical Physics,
Vol. 26,
Issue. 9,
p.
2308.
Kelly, P F
and
Mann, R B
1987.
Static spherically symmetric solutions in a new algebraically extended theory of gravity.
Classical and Quantum Gravity,
Vol. 4,
Issue. 6,
p.
1593.
Gegenberg, J.
Kelly, P. F.
Mann, R. B.
and
Vincent, D.
1988.
Theories of gravitation in two dimensions.
Physical Review D,
Vol. 37,
Issue. 12,
p.
3463.
Mann, R B
1989.
New ghost-free extensions of general relativity.
Classical and Quantum Gravity,
Vol. 6,
Issue. 1,
p.
41.
Kalinowski, M. W.
1991.
Nonsymmetric Kaluza-Klein and Jordan-Thiry theory in a general non-Abelian case.
International Journal of Theoretical Physics,
Vol. 30,
Issue. 3,
p.
281.
Kalinowski, M. W.
1992.
The nonsymmetric Kaluza-Klein (Jordan-Thiry) theory in the electromagnetic case.
International Journal of Theoretical Physics,
Vol. 31,
Issue. 4,
p.
611.
Cornish, Neil J.
and
Moffat, John W.
1994.
Nonsingular gravity without black holes.
Journal of Mathematical Physics,
Vol. 35,
Issue. 12,
p.
6628.
Cornish, Neil J.
and
Moffat, John W.
1994.
A non-singular theory of gravity?.
Physics Letters B,
Vol. 336,
Issue. 3-4,
p.
337.
Burko, Lior M.
and
Ori, Amos
1995.
On the Formation of Black Holes in Nonsymmetric Gravity.
Physical Review Letters,
Vol. 75,
Issue. 13,
p.
2455.
Galvagno, Mariano
and
Giribet, Gastón
2005.
The particle problem in classical gravity: a historical note on 1941.
European Journal of Physics,
Vol. 26,
Issue. 6,
p.
S97.
POPŁAWSKI, NIKODEM J.
2007.
ON THE NONSYMMETRIC PURELY AFFINE GRAVITY.
Modern Physics Letters A,
Vol. 22,
Issue. 36,
p.
2701.
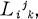 , where
, where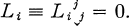
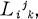 are independently varied, the above authors obtain the equivalent of the following field equations:
are independently varied, the above authors obtain the equivalent of the following field equations: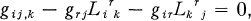
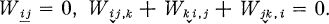
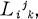 and the notation
and the notation