Article contents
Functional Equations, Distributions and Approximate Identities
Published online by Cambridge University Press: 20 November 2018
Extract
The subject of this paper is the use of the theory of Schwartz distributions and approximate identities in studying the functional equation
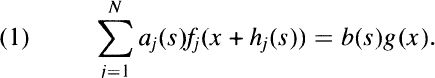
The aj’s and b are complex-valued functions defined on a neighbourhood, U, of 0 in Rm, hj. U → Rn with hj(0) = 0 and fj, g: Rn → C for 1 ≦ j ≦ N. In most of what follows the aj's and hj's are assumed smooth and may be thought of as given. The fj‘s, b and g may be thought of as the unknowns. Typically we are concerned with locally integrable functions f1, … , fN such that, for each s in U, (1) holds for a.e. (almost every) x ∈ Rn, in the sense of Lebesgue measure.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1990
References
- 6
- Cited by


