Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T15:56:35.850Z Has data issue: false hasContentIssue false
  • English
  • Français

Fuchsian Embeddings in the Bianchi Groups

Published online by Cambridge University Press:  20 November 2018

Benjamin Fine
Benjamin Fine*
Affiliation:
Fairfield University, Fairfield, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If d is a positive square free integer we let Od be the ring of integers in 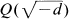and we let Γd = PSL2(Od), the group of linear fractional transformations

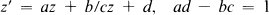
and entries from Od {if d = 1, ad – bc = ±1}. The Γd are called collectively the Bianchi groups and have been studied extensively both as abstract groups and in automorphic function theory {see references}. Of particular interest has been Γ1 – the Picard group. Group theoretically Γ1, is very similar to the classical modular group M = PSL2(Z) both in its total structure [4, 6], and in the structure of its congruence subgroups [8]. Where Γ1 and M differ greatly is in their action on the complex place C. M is Fuchsian and therefore acts discontinuously in the upper half-plane and every subgroup has the same property.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 6 , 01 December 1987 , pp. 1434 - 1445
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Best, L. A., On torsion-free discrete subgroups of PSL2(C) with compact orbit space, Can J. Math. 23 (1971), 451–460.Google Scholar
2. Brunner, A. M., Frame, M., Lee, Y. W. and Wielenberg, N. J., Classifying torsion-free subgroups of the Picard group, Trans, of the A. M. S. 282 (1984), 205–235.Google Scholar
3. Brunner, A. M., Lee, Y. W. and Wielenberg, N. J., Polyhedral groups and graph amalgamation products, to appear.CrossRefGoogle Scholar
4. Fine, B., The structure of PSL2(R); R the ring of integers in a Euclidean quadratic imaginary number field, Ph.D. thesis, New York University (1973).CrossRefGoogle Scholar
5. Fine, B., The structure of PSL2(R), Ann. of Math. Study. 79 (1974), 145–170.Google Scholar
6. Fine, B., The HNN and generalized free and generalized free product structure of certain linear groups, Bull. A.M. S. 81 (1975), 413–416.Google Scholar
7. Fine, B., Fuchsian subgroups of the Picard group, Can. J. Math. 28 (1976), 481–486.Google Scholar
8. Fine, B., Congruence subgroups of the Picard group, Can. J. Math. 32 (1979), 1474–1481.Google Scholar
9. Fine, B., Groups whose torsion-free subgroups are free, Bull. Acad. Sin. 12 (1984), 31–36.Google Scholar
10. Floge, D., Zur struktur der PSL2 uber einegen imaginar quadratischen Zahlringen, Math Z. 183 (1983), 255–279.Google Scholar
11. Grunewald, F. and Schwermer, J., Free non-abelian quotients of SL2 over orders of imaginary quadratic number fields, J. of Alg. 69 (1981), 162–175.Google Scholar
12. Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup, Tran. A. M. S. 150 (1970), 227–255.Google Scholar
13. Karrass, A. and Solitar, D., Subgroups of HNN groups and groups with one defining relation, Can. J. Math. 23 (1971), 627–643.Google Scholar
14. Lehner, J., Discontinuous groups and automorphic functions, Math Surveys 8 (Amer. Math. Soc., Providence R. I., 1964).CrossRefGoogle Scholar
15. Lyndon, R. and Schupp, P., Combinatorial group theory, (Springer-Verlag, New York, 1977).Google Scholar
16. Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory, (Wiley Interscience, New York, 1966).Google Scholar
17. Maskit, B., On a class of Kleinian groups, Ann. Academia Scient. Fennicae I, Mathematica, Helsinki (1969), 1–7.Google Scholar
18. Maclachlan, C., Fuchsian subgroups of the groups PSL2(Od), to appear.Google Scholar
19. Mennicke, J., A note on regular coverings of closed orientable surfaces, Proc. Glasgow Math. Soc. 5(1969), 49–66.Google Scholar
20. Newman, M., Integral matrices, (Academic Press, New York, 1972).Google Scholar
21. Serre, J. P., Trees, (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
22. Swan, R. G., Generators and relations for certain special linear groups, Adv. in Math. 6 (1971), 1–77.Google Scholar
23. Waldinger, H., On the subgroups of the Picard group, Proc. A. M. S. 16 (1965), 1375–1378.Google Scholar