Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-20T12:25:38.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Frobenius Distribution for Quotients of Fermat Curves of Prime Exponent

Published online by Cambridge University Press:  20 November 2018

Francesc Fité ,
Josep González  and
Joan-Carles Lario
Francesc Fité
Affiliation:
Institut für Experimentelle Mathematik/Fakultät für Mathematik, Universität Duisburg-Essen, D-45127 Essen, Germany e-mail: [email protected]
Josep González
Affiliation:
Departament de Matemàtica Aplicada IV, Universitat Politècnica de Catalunya, Av. Víctor Balaguer s/n., E-08800 Vilanova i la Geltrύ, Catalonia e-mail: [email protected]
Joan-Carles Lario
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, Edifici Omega-Campus Nord, Jordi Girona 1-3, E-08034 Barcelona, Catalonia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $C$ denote the Fermat curve over 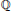$\mathbb{Q}$ of prime exponent $l$ . The Jacobian 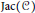$\text{Jac(}C\text{)}$ of $C$ splits over 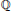$\mathbb{Q}$ as the product of Jacobians $\text{Jac(}{{C}_{k}})$ , 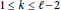$1\,\le \,k\,\le \,\ell \,-\text{2}$ , where 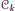${{C}_{k}}$ are curves obtained as quotients of $C$ by certain subgroups of automorphisms of $C$ . It is well known that $\text{Jac(}{{C}_{k}}\text{)}$ is the power of an absolutely simple abelian variety 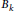${{B}_{k}}$ with complex multiplication. We call degenerate those pairs 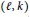$(l,\,k)$ for which 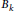${{B}_{k}}$ has degenerate 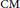$\text{CM}$ type. For a non-degenerate pair 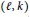$(l,\,k)$ , we compute the Sato–Tate group of $\text{Jac(}{{C}_{k}}\text{)}$ , prove the generalized Sato–Tate Conjecture for it, and give an explicit method to compute the moments and measures of the involved distributions. Regardless of whether 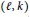$(l,\,k)$ is degenerate, we also obtain Frobenius equidistribution results for primes of certain residue degrees in the $l$ -th cyclotomic field. Key to our results is a detailed study of the rank of certain generalized Demjanenko matrices.

Keywords

11D4111M5011G1014G10Sato–Tate groupFermat curveFrobenius distribution
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 361 - 394
Copyright
Copyright © Canadian Mathematical Society 2016

References

[BGK03] Banaszak, G., Gajda, W., Krasoń, P., On Galois representations for abelian varieties with real and complex multiplications. J. Number Theory 100(2003), no. 1,117–132.http://dx.doi.Org/10.1016/SOO22-314X(02)00121-X Google Scholar
[BK15] Banaszak, G. and Kedlaya, K. S., An algebraic Sato-Tate group and Sato-Tate conjecture. Indiana Univ. Math. J. 64(2015), no. 1, 245–274.http://dx.doi.Org/10.1512/iumj.2O15.64.5438 Google Scholar
[BrüO4] Brünjes, L., Forms of Fermat equations and their zeta functions. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2004.http://dx.doi.Org/10.1142/9789812561800 Google Scholar
[Del82] Deligne, P., Hodge cycles on abelian varieties. In: Hodge cycles, motives, and Shimura varieties, Lecture Notes in Math., 900, Springer, 1982, pp. 9–100.Google Scholar
[Doh94] Dohmae, K., Demjanenko matrix for imaginary Abelian fields of odd conductors. Proc. Japan Acad. Ser. A Math. Sci. 70(1994), no. 9, 292–294.http://dx.doi.Org/10.3792/pjaa.70.292 Google Scholar
[Fitl5] Fité, F., Equidistribution, L-functions and Sato-Tate groups. Contemp. Math. 649(2015), 63–88.Google Scholar
[FKRS12] Fité, F., Kedlaya, K. S., Rotger, V., Sutherland, A. V., Sato-Tate distributions and Galois endomorphism modules in genus 2. Compositio Math. 148(2012), no. 5,1390–1442.http://dx.doi.org/10.1112/S0010437X12000279 Google Scholar
[FS14] Fité, F. and Sutherland, A.V., Sato-Tate distributions of twists of y2 = x5 − x and y2 = x6 + 1. Algebra Number Theory 8(2014), no. 3, 543–585.http://dx.doi.Org/10.2140/ant.2014.8.543 Google Scholar
[FS16] Fité, F. and Shparlinski, I. E., On the singularity of the Demjanenko matrix of quotients of Fermat curves. Proc. Amer. Math. Soc. 144(2016), no. 1, 55–63.http://dx.doi.Org/10.1090/prod2717 Google Scholar
[Gon99] González, J., Fermât facobians of prime degree over finite fields. Canad. Math. Bull. 42(1999), no. 1, 78–86.http://dx.doi.org/10.4153/CMB-1999-009-7 Google Scholar
[Gre80] Greenberg, R., On the facobian variety of some algebraic curves. Compositio Math. 42(1980/81), no. 3, 345–359.Google Scholar
[Gro78] Gross, B. H., On the periods of Abelian integrals and a formula ofChowla and Selberg. Invent. Math. 45(1978), no. 2, 193–211.http://dx.doi.Org/10.1007/BF01390273 Google Scholar
[Gr78] Gross, B. H and Rohrlich, D. E, Some results on the Mordell-Weil group of the facobian of the Fermât curve. Invent. Math. 44(1978), no. 3, 201–224.http://dx.doi.org/10.1007/BF01403161 Google Scholar
[Has55] Hasse, H., Zetafunktion und L-Funktionen zu einem arithmetischen Funktionenkorper vom Fermatschen Typus. Abh. Deutsch. Akad. Wiss. Berlin. Kl. Math. Nat. 1954(1954), no. 4.Google Scholar
[Haz90] Hazama, F., Demjanenko matrix, class number, and Hodge group. J. Number Theory 34(1990), no. 2, 174–177. http://dx.doi.Org/10.1016/0022-314X(90)90147-J Google Scholar
[Hec20] Hecke, E., Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen. Math. Z. 6(1920), no. 1-2,11–51. http://dx.doi.Org/10.1007/BF01202991Google Scholar
[Johl3] Johansson, C., On the Sato-Tate conjecture for non-generic abelian surfaces, with an Appendix by Francesc Fité. To appear in Trans. Amer. Math. Soc. arxiv:1307.6478 Google Scholar
[KR78] Koblitz, N. and Rohrlich, D., Simple factors in the facobian of a Fermât curve. Canad. J. Math. 30(1978), no. 6, 1183–1205.http://dx.doi.org/10.4153/CJM-1978-099-6 Google Scholar
[KS09] Kedlaya, K. S. and Sutherland, A. V., Hyperelliptic curves, L-polynomials, and random matrices. In: Arithmetic, geometry, cryptography, and coding theory, Contemp. Math., 487, American Mathematical Society, Providence, RI, 119–162.http://dx.doi.Org/10.1090/conm/487/09529 Google Scholar
[Kub65] Kubota, T. , On the field extension by complex multiplication. Trans. Amer. Math. Soc. 118(1965), 113–122.http://dx.doi.org/10.1090/S0002-9947-1965-0190144-8 Google Scholar
[Lan78] Lang, S., Cyclotomic fields. Graduate Texts in Mathematics, 59, Springer-Verlag, New York-Heidelberg- Berlin, 1978.Google Scholar
[Leo62] Leopoldt, H. W., Zur Arithmetik in Abelschen Körper. J. Reine Angew. Math. 209(1962), 54–71.Google Scholar
[Mai89] Mai, L., Lower Bounds for the ranks of CM types. J. Number Theory 32(1989), no. 2, 192–202.http://dx.doi.org/10.1016/0022-314X(89)90025-5 Google Scholar
[Rib80] Ribet, K. A., Division fields of abelian varieties with complex multiplication. Abelian functions and transcendental numbers (Colloq., Étole Polytech., Palaiseau, 1979), Mém. Soc. Math. France (N.S.), 1980/81, no. 2, pp. 75–94.Google Scholar
[Ser68] Serre, J.-P., Abelian ℓ-adic representations and elliptic curves. Research Notes in Mathematics, 7, A K Peters, Wellesley, MA, 1998.Google Scholar
[Ser77] Serre, J.-P., Linear representations of finite groups. Graduate Texts in Mathematics, 42, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
[Serl2] Serre, J.-P., Lectures on Nx(p). Chapman & Hall/CRC Research Notes in Mathematics, 11, CRC Press, Boca Raton, FL, 2012.Google Scholar
[SS95] Sands, J. W. and Schwartz, W., A Demjanenko matrix for abelian fields of prime power conductor. J. Number Theory 52(1995), no. 1, 85–97.http://dx.doi.org/10.1006/jnth.1995.1057 Google Scholar
[ST61] Shimura, G. and Taniyama, Y., Complex multiplication of abelian varieties and its applications to number theory. The Mathematical Society of Japan, Tokyo, 1961.Google Scholar
[Sti90] Stickelberger, L., Über eine Verallgemeinerung der Kreistheilung. Math. Ann. 37(1890), no. 3, 321–367.http://dx.doi.org/10.1007/BF01721360 Google Scholar
[Tan96] Tankaeev, S. G., On the Mumford-Tate conjecture for abelian varieties. Algebraic geometry 4, J. Math Sci. 81(1996), no. 3, 2719–2737.http://dx.doi.org/10.1007/BF02362337 Google Scholar
[Wei52] Weil, A., Jacobi sums as “Grössencharaktere”. Trans. Amer. Math. Soc. 73(1952), 487–495.Google Scholar
[Yul5] Yu, C.-F., A note on the Mumford-Tate conjecture for CM abelian varieties. Taiwanese J. Math. 19(2015), no. 4, 1073–1084.Google Scholar