Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-18T20:39:51.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Multivariate w*-Semicrossed Products: Reflexivity and the Bicommutant Property

Published online by Cambridge University Press:  20 November 2018

Robert T. Bickerton  and
Evgenios T. A. Kakariadis
Robert T. Bickerton
Affiliation:
Newcastle University, Newcastle, NE1 7 RU, United Kingdom, e-mail: [email protected] , [email protected]
Evgenios T. A. Kakariadis
Affiliation:
Newcastle University, Newcastle, NE1 7 RU, United Kingdom, e-mail: [email protected] , [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study 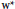${{\text{w}}^{*}}$-semicrossed products over actions of the free semigroup and the free abelian semigroup on (possibly non-selfadjoint) 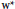${{\text{w}}^{*}}$-closed algebras. We show that they are reflexive when the dynamics are implemented by uniformly bounded families of invertible row operators. Combining with results of Helmer, we derive that 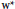${{\text{w}}^{*}}$-semicrossed products of factors (on a separableHilbert space) are reflexive. Furthermore, we show that 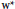${{\text{w}}^{*}}$-semicrossed products of automorphic actions on maximal abelian self adjoint algebras are reflexive. In all cases we prove that the 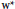${{\text{w}}^{*}}$-semicrossed products have the bicommutant property if and only if the ambient algebra of the dynamics does also.

Keywords

47A1547L6547L7547L80reflexivitysemicrossed product
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1201 - 1235
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Anoussis, M., Katavolos, A., and Todorov, I. G., Operator algebras from the discrete Heisenberg semigroup. Proc. Edinb. Math. Soc. (2) 55 (2012), 1–22. http://dx.doi.Org/10.1017/S0013091510000143Google Scholar
[2] Arias, A. and Popescu, G., Factorization and reflexivity on Fock spaces. Integral Equations Operator Theory 23 (1995), 268–286. http://dx.doi.Org/10.1007/BF01198485Google Scholar
[3] Arveson, W., Operator algebras and invariant subspaces. Ann. of Math. 100 (1974), no. 2, 433–532. http://dx.doi.Org/10.2307/1970956Google Scholar
[4] Arveson, W., Interpolation problems in nest algebras. J. Functional Analysis 20 (1975), 208–233. http://dx.doi.Org/10.1016/0022-1236(75)90041-5Google Scholar
[5] Arveson, W., Ten lectures on operator algebras. CBMS Regional Conference Series in Mathematics, 55, American Mathematical Society, Providence, RI, 1984. http://dx.doi.Org/10.109O/cbms/O55Google Scholar
[6] Arveson, W., Continuous analogues of Fock space. Mem. Amer. Math. Soc. 80 (1989), no. 409. http://dx.doi.Org/10.1090/memo/0409Google Scholar
[7] Bercovici, H., Hyper-reflexivity and the factorization of linear functionals. J. Funct. Anal. 158 (1998), 242–252. http://dx.doi.org/10.1006/jfan.1998.3288Google Scholar
[8] Brown, S. W., Some invariant subspaces for subnormal operators. Integral Equations Operator Theory 1 (1978), 310–333. http://dx.doi.org/10.1007/BF01682842Google Scholar
[9] Conway, J. B., A course in operator theory. Graduate Studies in Mathematics Series, 21, American Mathematical Society, Providence, RI, 1991.Google Scholar
[10] Courtney, D., Muhly, P. S., and Schmidt, W., Composition operators and endomorphisms. Complex Anal. Oper. Theory 6 (2012), no. 1, 163–188. http://dx.doi.Org/10.1007/s11785-010-0075-4Google Scholar
[11] Cuntz, J., K-theoryfor certain C*-algebras, Ann. of Math. (2) 113 (1981), 181–197. http://dx.doi.Org/10.2307/1971137Google Scholar
[12] Davidson, K. R., The distance to the analytic Toeplitz operators. Illinois J. Math. 31 (1987), 265–273.Google Scholar
[13] Davidson, K. R., Nest algebras. Pitman Research Notes in Mathematics Series, 191, Longman Scientific & Technical, 1988.Google Scholar
[14] Davidson, K. R., Fuller, A. H., and Kakariadis, E. T. A., Semicrossed products of operator algebras by semigroups. Mem. Amer. Math. Soc. 247 (2017), no. 1168.Google Scholar
[15] Davidson, K. R., Semicrossed products of operator algebras: a survey. New York J. Math., to appear. arxiv:1404.1907Google Scholar
[16] Davidson, K. R., Katsoulis, E. G., and Pitts, D. R., The structure of free semigroup algebras. J. Reine Angew. Math. 533 (2001), 99–125. http://dx.doi.Org/10.1515/crll.2OO1.028Google Scholar
[17] Davidson, K. R. and Pitts, D. R., Nevanlinna-Pick Interpolation for non-commutative analytic Toeplitz algebras. Integral Equations Operator Theory 31 (1998), 321–337. http://dx.doi.Org/10.1007/BF01195123Google Scholar
[18] Davidson, K. R. and Pitts, D. R., Invariant subspaces and hyper-reflexivity for free semigroup algebras. Proc. London Math. Soc. 78 (1999), 401–430. http://dx.doi.Org/10.1112/S002461159900180XGoogle Scholar
[19] Fuller, A. H. and Kennedy, M., Isometric tuples are hyperreflexive. Indiana Univ. Math. J. 62 (2013), 1679–1689. http://dx.doi.org/10.1512/iumj.2013.62.5144Google Scholar
[20] Gipson, P., Invariant basis number for C*-algebras. Illinois J. Mathematics 59 (2015), 85–98.Google Scholar
[21] Hasegawa, K., Essential commutants of semicrossed products. Canad. Math. Bull. 58 (2015), 91–104. http://dx.doi.Org/10.4153/CMB-2O14-057-xGoogle Scholar
[22] Helmer, L., Reflexivity of non-commutative Hardy algebras. J. Funct. Anal. 272 (2017), 2752–2794. http://dx.doi.Org/10.1016/j.jfa.2O16.12.004Google Scholar
[23] Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. II, Graduate Studies in Mathematics, 16, American Mathematical Society, Providence, RI, 1997.Google Scholar
[24] Kakariadis, E. T. A., Semicrossed products and reflexivity. J. Operator Theory 67 (2012), 379–395.Google Scholar
[25] Kakariadis, E. T. A., The Dirichlet property for tensor algebras. Bull. Lond. Math. Soc. 45 (2013), 1119–1130. http://dx.doi.Org/10.1112/blms/bdtO41Google Scholar
[26] Kakariadis, E. T. A. and Katsoulis, E. G., Isomorphism invariants for multivariable C*-dynamics. J. Noncommut. Geom. 8 (2014), 771–787. http://dx.doi.Org/10.4171/JNCC/170Google Scholar
[27] Kakariadis, E. T. A. and Peters, J. R., Representations of C*-dynamical systems implemented by Cuntz families. Munster J. Math. 6 (2013), 383–411.Google Scholar
[28] Kakariadis, E. T. A. and Peters, J. R., Ergodic extensions of endomorphisms. Bull. Aust. Math. Soc. 93 (2016), 307–320. http://dx.doi.org/10.1017/S0004972715001161Google Scholar
[29] Kraus, J. and Larson, D., Reflexivity and distance formulae. Proc. London Math. Soc. 53 (1986), 340–356. http://dx.doi.Org/10.1112/plms/s3-53.2.340Google Scholar
[30] Kastis, L. and Power, S. C., The operator algebra generated by the translation, dilation and multiplication semigroups. J. Funct. Anal. 269 (2015), 3316–3335. http://dx.doi.Org/10.1016/j.jfa.2O15.08.005Google Scholar
[31] Katavolos, A. and Power, S. C., Translation and dilation invariant subspaces ofL (R). J. Reine Angew. Math. 552 (2002), 101–129. http://dx.doi.org/10.1515/crll.2002.087Google Scholar
[32] Kennedy, M., Wandering vectors and the reflexivity of free semigroup algebras. J. Reine Angew. Math. 653 (2011), 47–73. http://dx.doi.Org/10.1515/CRELLE.2O11.019Google Scholar
[33] Kribs, D. W. and Power, S. C., Free semigroupoid algebras. J. Ramanujan Math. Soc. 19 (2004), 117–159.Google Scholar
[34] Kribs, D. W., Levene, R. H., and Power, S. C., Commutants of weighted shift directed graph operator algebras. Proc. Amer. Math. Soc. 145 (2017), 3465–3480. http://dx.doi.Org/10.1090/proc/13477Google Scholar
[35] Laca, M., Endomorphisms of B(J﹛) and Cuntz algebras. J. Operator Th. 30 (1993), 85–108.Google Scholar
[36] Loginov, A. N. and SuFman, V. S., Hereditary and intermediate reflexivity ofW*-algebras. Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 1260–1273.Google Scholar
[37] McAsey, M., Muhly, P. S., and Saito, K.-S., Nonselfadjoint crossed products (invariant subspaces and maximality). Trans. Amer. Math. Soc. 248:2 (1979), 381–409. http://dx.doi.org/10.1090/S0002-9947-1979-0522266-3Google Scholar
[38] Muhly, P. S. and Solel, B., Hardy algebras, W*-correspondences and interpolation theory. Math. Ann. 330 (2004), 353–415. http://dx.doi.Org/10.1007/s00208-004-0554-xGoogle Scholar
[39] Peligrad, C., Reflexive operator algebras on noncommutative Hardy spaces. Math. Ann. 253 (1980), 165–175. http://dx.doi.Org/10.1007/BF01 578912Google Scholar
[40] Peligrad, C., Invariant subspaces of algebras of analytic elements associated with periodic flows on W*-algebras. Houston J. Math. 42 (2016), 1331–1344.Google Scholar
[41] Popescu, G., von Neumann inequality for (23(Of )“)i. Math. Scand. 68 (1991), 292–304. http://dx.doi.org/10.7146/math.scand.a-12363Google Scholar
[42] Ptak, M., On the reflexivity of pairs of isometries and of tensor products of some operator algebras. Studia Math. 83 (1986), 47–55; erratum Studia Math. 103 (1992), 221–223.Google Scholar
[43] Radjavi, H. and Rosenthal, P., On invariant subspaces and reflexive algebras. Amer. J. Math. 91 (1969), 683–692. http://dx.doi.org/10.2307/2373347Google Scholar
[44] Radjavi, H. and Rosenthal, P., Invariant subspaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 77, Springer-Verlag, New York-Heidelberg, 1973.Google Scholar
[45] Sarason, D., Invariant subspaces and unstarred operator algebras. Pacific J. Math. 17 (1966), 511–517. http://dx.doi.org/10.2140/pjm.1966.17.511Google Scholar