Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-08T05:32:24.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Lattices Generated by Partially Ordered Sets and Preserving Bounds

Published online by Cambridge University Press:  20 November 2018

R. A. Dean
R. A. Dean*
Affiliation:
California Institute of Technology Pasadena, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A construction of the free lattice generated by a partially ordered set P and preserving every least upper bound (lub) and greatest lower bound (glb) of pairs of elements existing in P has been given by Dilworth (2, pp. 124-129) and, when P is finite, by Gluhov (5).

The results presented here construct the free lattice FL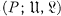 generated by the partially ordered set P and preserving

(1) the ordering of P

(2) those lub's of a family 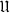of finite subsets of P which possess lub's in P

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 136 - 148
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Dean, R. A., Completely free lattices generated by partially ordered sets, Trans. Amer. Math. Soc, 83 (1956), 238–249.Google Scholar
2. Dilworth, R. P., Lattices with unique complements, Trans. Amer. Math. Soc, 57 (1945), 123–154.Google Scholar
3. Dilworth, R. P. and Peter Crawley, Decomposition theory for lattices without chain conditions, Trans. Amer. Math. Soc, 96 (1960), 1–22.Google Scholar
4. Evans, T., The word problem for abstract algebras, J. London Math. Soc, 26 (1951), 64–71.Google Scholar
5. Gluhov, M. M., On the problem of isomorphism of lattices, Dokl. Akad. Nauk SSSR, 132 (1960), 254–256; Soviet Math. 1 (1960), 519-522.Google Scholar
6. Yu. Sorkin, I., On the embedding of latticoids in lattices, Dokl. Akad. Nauk SSSR (N.S.), 95 (1954), 931–934.Google Scholar
7. Whitman, P. M., Free lattices I, Ann. of Math. (2), 42 (1941), 325–330.Google Scholar