Hostname: page-component-7479d7b7d-t6hkb Total loading time: 0 Render date: 2024-07-09T00:45:03.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Group Algebras in Division Rings with Valuation II

Part of: Division rings and semisimple Artin rings Rings and algebras arising under various constructions Rings and algebras with additional structure Conditions on elements

Published online by Cambridge University Press:  05 July 2019

Javier Sánchez
Javier Sánchez*
Affiliation:
Department of Mathematics - IME, University of São Paulo, Rua do Matão 1010, São Paulo, SP, 05508-090, Brazil Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We apply the filtered and graded methods developed in earlier works to find (noncommutative) free group algebras in division rings.

If 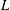$L$ is a Lie algebra, we denote by 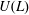$U(L)$ its universal enveloping algebra. P. M. Cohn constructed a division ring 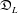$\mathfrak{D}_{L}$ that contains 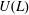$U(L)$. We denote by 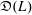$\mathfrak{D}(L)$ the division subring of 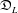$\mathfrak{D}_{L}$ generated by 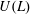$U(L)$.

Let 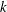$k$ be a field of characteristic zero, and let 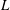$L$ be a nonabelian Lie 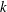$k$-algebra. If either 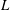$L$ is residually nilpotent or 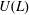$U(L)$ is an Ore domain, we show that 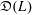$\mathfrak{D}(L)$ contains (noncommutative) free group algebras. In those same cases, if 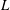$L$ is equipped with an involution, we are able to prove that the free group algebra in 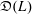$\mathfrak{D}(L)$ can be chosen generated by symmetric elements in most cases.

Let 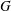$G$ be a nonabelian residually torsion-free nilpotent group, and let 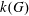$k(G)$ be the division subring of the Malcev–Neumann series ring generated by the group algebra 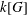$k[G]$. If 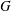$G$ is equipped with an involution, we show that 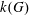$k(G)$ contains a (noncommutative) free group algebra generated by symmetric elements.

Keywords

division ringfiltered ringgraded ringvaluationring with involutionfree group algebrauniversal enveloping algebraordered group

MSC classification

Primary: 16K40: Infinite-dimensional and general
Secondary: 16W70: Filtered rings; filtrational and graded techniques 16W60: Valuations, completions, formal power series and related constructions 16W10: Rings with involution; Lie, Jordan and other nonassociative structures 16S10: Rings determined by universal properties (free algebras, coproducts, adjunction of inverses, etc.) 16S30: Universal enveloping algebras of Lie algebras 16U20: Ore rings, multiplicative sets, Ore localization
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1463 - 1504
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by FAPESP-Brazil, Proj. Temático 2015/09162-9, by Grant CNPq 307638/2015-4 and by MINECO-FEDER (Spain) through project numbers MTM2014-53644-P and MTM2017-83487-P.

References

Bell, J. and Rogalski, D., Free subalgebras of quotient rings of ore extensions. Algebra Number Theory 6(2012), no. 7, 1349–1367. https://doi.org/10.2140/ant.2012.6.1349CrossRefGoogle Scholar
Bell, J. P. and Gonçalves, J. Z., Free algebras and free groups in Ore extensions and free group algebras in division rings. J. Algebra 455(2016), 235–250. https://doi.org/10.1016/j.jalgebra.2016.02.011CrossRefGoogle Scholar
Bois, J.-M., Corps enveloppants des algèbres de type Witt. J. Algebra 269(2003), no. 2, 669–700. https://doi.org/10.1016/S0021-8693(03)00402-2CrossRefGoogle Scholar
Cauchon, G., Corps minimaux contenant l’algèbre du groupe libre à deux générateurs. Comm. Algebra 23(1995), no. 2, 437–454. https://doi.org/10.1080/00927879508825230CrossRefGoogle Scholar
Chiba, K., Free subgroups and free subsemigroups of division rings. J. Algebra 184(1996), no. 2, 570–574. https://doi.org/10.1006/jabr.1996.0275CrossRefGoogle Scholar
Cimprič, J., Free skew fields have many ∗-orderings. J. Algebra 280(2004), no. 1, 20–28. https://doi.org/10.1016/j.jalgebra.2004.01.033CrossRefGoogle Scholar
Cohn, P. M., Skew Fields. Theory of general division rings. Encyclopedia of Mathematics and its Applications, 57, Cambridge University Press, Cambridge, 1995. https://doi.org/10.1017/CBO9781139087193CrossRefGoogle Scholar
Cohn, P. M., On the embedding of rings in skew fields. Proc. Lond. Math. Soc. 11(1961), no. 3, 511–530. https://doi.org/10.1112/plms/s3-11.1.511CrossRefGoogle Scholar
Dixmier, J., Enveloping algebras. Graduate Studies in Mathematics, 11, American Mathematical Society, Providence, RI, 1996. https://doi.org/10.1090/gsm/011Google Scholar
Ferreira, V. O., Gonçalves, J. Z., and Sánchez, J., Free symmetric algebras in division rings generated by enveloping algebras of Lie algebras. Internat. J. Algebra Comput. 25(2015), no. 6, 1075–1106. https://doi.org/10.1142/S0218196715500319CrossRefGoogle Scholar
Ferreira, V. O., Fornaroli, É. Z., and Gonçalves, J. Z., Free algebras in division rings with an involution. J. Algebra 509(2018), 292–306. https://doi.org/10.1016/j.jalgebra.2018.01.025CrossRefGoogle Scholar
Ferreira, V. O. and Gonçalves, J. Z., Free symmetric and unitary pairs in division rings infinite-dimensional over their centers. Israel J. Math. 210(2015), no. 1, 297–321. https://doi.org/10.1007/s11856-015-1253-xCrossRefGoogle Scholar
Ferreira, V. O., Gonçalves, J. Z., and Sánchez, J., Free symmetric group algebras in division rings generated by poly-orderable groups. J. Algebra 392(2013), 69–84. https://doi.org/10.1016/j.jalgebra.2013.06.016CrossRefGoogle Scholar
Ferreira, V. O., Gonçalves, J. Z., and Sánchez, J., Free symmetric and unitary pairs in the field of fractions of torsion-free nilpotent group algebras. Algebr. Represent. Theor. (2019), https://doi.org/10.1007/s10468-019-09866-8Google Scholar
Fuchs, L., Partially ordered algebraic systems. Pergamon Press, Oxford, 1963.Google Scholar
Gonçalves, J. Z., Free groups in subnormal subgroups and the residual nilpotence of the group of units of group rings. Canad. Math. Bull. 27(1984), no. 3, 365–370. https://doi.org/10.4153/CMB-1984-055-6CrossRefGoogle Scholar
Gonçalves, J. and Shirvani, M., On free group algebras in division rings with uncountable center. Proc. Amer. Math. Soc. 124(1996), no. 3, 685–687. https://doi.org/10.1090/S0002-9939-96-03032-8CrossRefGoogle Scholar
Gonçalves, J. and Shirvani, M., A survey on free objects in division rings and in division ring with an involution. Comm. Algebra 40(2012), no. 5, 1704–1723. https://doi.org/10.1080/00927872.2011.554934CrossRefGoogle Scholar
Hughes, I., Division rings of fractions for group rings. Comm. Pure Appl. Math. 23(1970), 181–188. https://doi.org/10.1002/cpa.3160230205CrossRefGoogle Scholar
Jacobson, N., Lie algebras. Dover Publications Inc., New York, 1979.Google Scholar
Li, H. S., Note on microlocalizations of filtered rings and the embedding of rings in skewfields. Bull. Soc. Math. Belg. Sér. A 43(1991), no. 1–2, 49–57.Google Scholar
Lichtman, A. I., Free subgroups of normal subgroups of the multiplicative group of skew fields. Proc. Amer. Math. Soc. 71(1978), no. 2, 174–178. https://doi.org/10.2307/2042827CrossRefGoogle Scholar
Lichtman, A. I., Matrix rings and linear groups over a field of fractions of enveloping algebras and group rings. I. J. Algebra 88(1984), no. 1, 1–37. https://doi.org/10.1016/0021-8693(84)90087-5CrossRefGoogle Scholar
Lichtman, A. I., Valuation methods in division rings. J. Algebra 177(1995), no. 3, 870–898. https://doi.org/10.1006/jabr.1995.1332CrossRefGoogle Scholar
Lichtman, A. I., Free subalgebras in division rings generated by universal enveloping algebras. Algebra Colloq. 6(1999), no. 2, 145–153.Google Scholar
Lichtman, A. I., On universal fields of fractions for free algebras. J. Algebra 231(2000), no. 2, 652–676. https://doi.org/10.1006/jabr.2000.8344CrossRefGoogle Scholar
Makar-Limanov, L., The skew field of fractions of the Weyl algebra contains a free noncommutative subalgebra. Comm. Algebra 11(1983), no. 17, 2003–2006. https://doi.org/10.1080/00927878308822945CrossRefGoogle Scholar
Makar-Limanov, L., On free subobjects of skew fields. In: Methods in ring theory (Antwerp, 1983). NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 129, Reidel, Dordrecht, 1984, pp. 281–285.CrossRefGoogle Scholar
Makar-Limanov, L., On group rings of nilpotent groups. Israel J. Math. 48(1984), no. 2–3, 244–248. https://doi.org/10.1007/BF02761167CrossRefGoogle Scholar
Makar-Limanov, L., On subalgebras of the first Weyl skewfield. Comm. Algebra 19(1991), no. 7, 1971–1982. https://doi.org/10.1080/00927879108824241CrossRefGoogle Scholar
Malcev, A. I., On the embedding of group algebras in division algebras. Doklady Akad. Nauk SSSR (N.S.) 60(1948), 1499–1501.Google Scholar
Marubayashi, H. and Van Oystaeyen, F., Prime divisors and noncommutative valuation theory. Lecture Notes in Mathematics, 2059, Springer, Heidelberg, 2012. https://doi.org/10.1007/978-3-642-31152-9CrossRefGoogle Scholar
Năstăsescu, C. and Van Oystaeyen, F., Methods of graded rings. Lecture Notes in Mathematics, 1836, Springer-Verlag, Berlin, 2004. https://doi.org/10.1007/b94904CrossRefGoogle Scholar
Neumann, B. H., On ordered division rings. Trans. Amer. Math. Soc. 66(1949), 202–252. https://doi.org/10.2307/1990552CrossRefGoogle Scholar
Passi, I. B. S., Group rings and their augmentation ideals. Lecture Notes in Mathematics, 715, Springer, Berlin, 1979.CrossRefGoogle Scholar
Passman, D. S., Infinite crossed products. Pure and Applied Mathematics, 135, Academic Press Inc., Boston, MA, 1989.Google Scholar
Quillen, D. G., On the associated graded ring of a group ring. J. Algebra 10(1968), 411–418. https://doi.org/10.1016/0021-8693(68)90069-0CrossRefGoogle Scholar
Sánchez, J., Free group algebras in Malcev–Neumann skew fields of fractions. Forum Math. 26(2014), no. 2, 443–466. https://doi.org/10.1515/form.2011.170CrossRefGoogle Scholar
Sánchez, J., Obtaining free group algebras in division rings generated by group graded rings. J. Algebra Appl. 17(2018), 1850194. https://doi.org/10.1142/S0219498818501943Google Scholar
Sánchez, J., Free group algebras in division rings with valuation I. J.  Algebra 531(2019), 221–248. https://doi.org/10.1016/j.jalgebra.2019.04.021CrossRefGoogle Scholar
Vergne, M., Cohomologie des algèbres de Lie nilpotentes. Application à l’étude de la variété des algèbres de Lie nilpotentes. Bull. Soc. Math. France 98(1970), 81–116.CrossRefGoogle Scholar