Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T16:34:37.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Bessel Laws

Published online by Cambridge University Press:  20 November 2018

T. Banica ,
S. T. Belinschi ,
M. Capitaine  and
B. Collins
T. Banica
Affiliation:
Department of Mathematics, Toulouse 3 University, Toulouse, France email: [email protected]@cict.fr
S. T. Belinschi
Affiliation:
Department of Mathematics, University of Saskatchewan, Saskatoon, SK email: [email protected]
M. Capitaine
Affiliation:
Department of Mathematics, Toulouse 3 University, Toulouse, France email: [email protected]@cict.fr
B. Collins
Affiliation:
Department of Mathematics, Lyon 1 University, France and University of Ottawa, Ottawa, ON email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

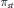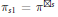We introduce and study a remarkable family of real probability measures ${{\pi }_{st}}$ that we call free Bessel laws. These are related to the free Poisson law $\pi $ via the formulae ${{\text{ }\!\!\pi\!\!\text{ }}_{s1}}={{\text{ }\!\!\pi\!\!\text{ }}^{\boxtimes s}}$ and 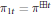$\text{ }\pi {{\text{ }}_{1t}}=\text{ }\pi {{\text{ }}^{\boxtimes }}^{t}$. Our study includes definition and basic properties, analytic aspects (supports, atoms, densities), combinatorial aspects (functional transforms, moments, partitions), and a discussion of the relation with random matrices and quantum groups.

Keywords

46L5415A5216W30Poisson lawBessel functionWishart matrixquantum group
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 1 , 01 February 2011 , pp. 3 - 37
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] D., Armstrong, Generalized noncrossing partitions and combinatorics of Coxeter groups. Mem. Amer. Math. Soc. 202(2009), no. 949.Google Scholar
[2] Banica, T., A note on free quantum groups. Ann. Math. Blaise Pascal 15(2008), no. 2, 135–146.Google Scholar
[3] Banica, T. and Bichon, J., Free product formulae for quantum permutation groups. J. Inst. Math. Jussieu 6(2007), no. 3, 381–414. doi:10.1017/S1474748007000072Google Scholar
[4] Banica, T., Bichon, J., and Collins, B., The hyperoctahedral quantum group. J. Ramanujan Math. Soc. 22(2007), no. 4, 345–384.Google Scholar
[5] Banica, T. and Collins, B., Integration over compact quantum groups. Publ. Res. Inst. Math. Sci. 43(2007), no. 2, 277–302. doi:10.2977/prims/1201011782Google Scholar
[6] Banica, T. and Collins, B., Integration over quantum permutation groups. J. Funct. Anal. 242(2007), no. 2, 641–657. doi:10.1016/j. jfa.2006.09.005Google Scholar
[7] Belinschi, S. T., The atoms of the free multiplicative convolution of two probability distributions. Integral Equations Operator Theory 46(2003), no. 4, 377–386. doi:10.1007/s00020-002-1145-4Google Scholar
[8] Belinschi, S. T. and H., Bercovici, Partially defined semigroups relative to multiplicative free convolution. Int. Math. Res. Not.2005, no. 2, 65–101. doi:10.1155/IMRN.2005.65Google Scholar
[9] Bercovici, H. and Pata, V., Stable laws and domains of attraction in free probability theory. Ann. of Math. 149(1999), no. 3, 1023–1060. doi:10.2307/121080Google Scholar
[10] Bercovici, H. and Voiculescu, D. V., Free convolution of measures with unbounded support. Indiana Univ. Math. J. 42(1993), no. 3, 733–773. doi:10.1512/iumj.1993.42.42033Google Scholar
[11] Biane, P., Some properties of crossings and partitions. Discrete Math. 175(1997), no. 1–3, 41–53. doi:10.1016/S0012-365X(96)00-2Google Scholar
[12] Bichon, J., Free wreath product by the quantum permutation group. Algebr. Represent. Theory 7(2004), no. 4, 343–362. doi:10.1023/B:ALGE.0000042148.97035. caGoogle Scholar
[13] Bisch, D. and Jones, V. F. R., Algebras associated to intermediate subfactors. Invent. Math. 128(1997), no. 1, 89–157. doi:10.1007/s002220050137Google Scholar
[14] Edelman, P. H., Chain enumeration and noncrossing partitions. Discrete Math. 31(1980), no. 2, 171–180. doi:10.1016/0012-365X(80)90033-3Google Scholar
[15] Graczyk, P., Letac, G., and Massam, H., The complex Wishart distribution and the symmetric group. Ann. Statist. 31(2003), no. 1, 287–309. doi:10.1214/aos/1046294466Google Scholar
[16] Haagerup, U. and Thorbjørnsen, S., Random matrices with complex Gaussian entries. Expo. Math. 21(2003), no. 4, 293–337. doi:10.1016/S0723-0869(03)80036-1Google Scholar
[17] Hiai, F. and Petz, D., The semicircle law, free random variables and entropy. Mathematical Surveys and Monographs, 77, American Mathematical Society, Providence, RI, 2000.Google Scholar
[18] Lehner, F., Cumulants in noncommutative probability theory. I. Noncommutative exchangeability systems. Math. Z. 248(2004), no. 1, 67–100. doi:10.1007/s00209-004-0653-0Google Scholar
[19] A. Mingo, J. and Nica, A., Annular noncrossing permutations and partitions, and second-order asymptotics for random matrices. Int. Math. Res. Not. 2004, no. 28, 1413–1460. doi:10.1155/S1073792804133023Google Scholar
[20] Nica, A. and Speicher, R., Lectures on the combinatorics of free probability. London Mathematical Society Lecture Note Series, 335, Cambridge University Press, Cambridge, 2006.Google Scholar
[21] Speicher, R., Multiplicative functions on the lattice of noncrossing partitions and free convolution. Math. Ann. 298(1994), no. 4, 611–628. doi:10.1007/BF01459754Google Scholar
[22] Speicher, R., Combinatorial theory of the free product with amalgamation and operator-valued free probability theory. Mem. Amer. Math. Soc. 132(1998), no. 627.Google Scholar
[23] Stanley, R. P., Parking functions and noncrossing partitions. Electron. J. Combin. 4(1997), no. 2, Research Paper 20.Google Scholar
[24] Voiculescu, D., Addition of certain noncommuting random variables. J. Funct. Anal. 66(1986), no. 3, 323–346. doi:10.1016/0022-1236(86)90062-5Google Scholar
[25] Voiculescu, D., Multiplication of certain noncommuting random variables. J. Operator Theory 18(1987), no. 2, 223–235.Google Scholar
[26] Voiculescu, D., Lectures on free probability theory. In: Lectures on probability theory and statistics, Lecture Notes in Math., 1738, Springer, Berlin, 2000, pp. 279–349.Google Scholar
[27] Voiculescu, D. V., Dykema, K. J., and Nica, A., Free random variables. A noncommutative probability approach to free products with applications to random matrices, operator algebras and harmonic analysis on free groups. CRM Monograph Series, 1, American Mathematical Society, Providence, RI, 1992.Google Scholar
[28] Wang, S., Quantum symmetry groups of finite spaces. Comm. Math. Phys. 195(1998), no. 1, 195–211. doi:10.1007/s002200050385Google Scholar
[29] Woronowicz, S. L., Compact matrix pseudogroups. Comm. Math. Phys. 111(1987), no. 4, 613–665. doi:10.1007/BF01219077Google Scholar
[30] Woronowicz, S. L., Tannaka-Krein duality for compact matrix pseudogroups. Twisted SU(N) groups. Invent. Math. 93(1988), no. 1, 35–76. doi:10.1007/BF01393687Google Scholar