Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strichartz, Robert S.
1997.
Piecewise linear wavelets on sierpinski gasket type fractals.
The Journal of Fourier Analysis and Applications,
Vol. 3,
Issue. 4,
p.
387.
Dalrymple, Kyallee
Strichartz, Robert S.
and
Vinson, Jade P.
1999.
Fractal differential equations on the Sierpinski gasket.
The Journal of Fourier Analysis and Applications,
Vol. 5,
Issue. 2-3,
p.
203.
Strichartz, Robert S.
1999.
Some Properties of Laplacians on Fractals.
Journal of Functional Analysis,
Vol. 164,
Issue. 2,
p.
181.
Strichartz, Robert S.
2000.
Mock Fourier series and transforms associated with certain Cantor measures.
Journal d'Analyse Mathématique,
Vol. 81,
Issue. 1,
p.
209.
Sabot, Christophe
2000.
Pure Point Spectrum for the Laplacian on Unbounded Nested Fractals.
Journal of Functional Analysis,
Vol. 173,
Issue. 2,
p.
497.
Teplyaev, Alexander
2000.
Gradients on Fractals.
Journal of Functional Analysis,
Vol. 174,
Issue. 1,
p.
128.
Oberlin, Richard
Street, Brian
and
Strichartz, Robert S.
2003.
Sampling on the Sierpinski Gasket.
Experimental Mathematics,
Vol. 12,
Issue. 4,
p.
403.
Needleman, Jonathan
Strichartz, Robert S
Teplyaev, Alexander
and
Yung, Po-Lam
2004.
Calculus on the Sierpinski gasket I: polynomials, exponentials and power series.
Journal of Functional Analysis,
Vol. 215,
Issue. 2,
p.
290.
Doty, David
Gu, Xiaoyang
Lutz, Jack H.
Mayordomo, Elvira
and
Moser, Philippe
2005.
Mathematical Foundations of Computer Science 2005.
Vol. 3618,
Issue. ,
p.
283.
Allen, M.R.
Cruttwell, G.S.H.
Hare, Kathryn E.
and
Rönning, J.-O.
2007.
Dimensions of fractals in the large.
Chaos, Solitons & Fractals,
Vol. 31,
Issue. 1,
p.
5.
Fan, Edward
Khandker, Zuhair
and
Strichartz, Robert S.
2009.
Harmonic Oscillators on Infinite Sierpinski Gaskets.
Communications in Mathematical Physics,
Vol. 287,
Issue. 1,
p.
351.
Schindler, Ian
and
Tintarev, Kyril
2009.
Semilinear equations on fractal blowups.
Journal of Mathematical Analysis and Applications,
Vol. 352,
Issue. 1,
p.
57.
DENG, QI-RONG
2009.
REVERSE ITERATED FUNCTION SYSTEM AND DIMENSION OF DISCRETE FRACTALS.
Bulletin of the Australian Mathematical Society,
Vol. 79,
Issue. 1,
p.
37.
Okoudjou, Kasso A.
Rogers, Luke G.
and
Strichartz, Robert S.
2009.
Generalized Eigenfunctions and a Borel Theorem on the Sierpinski Gasket.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 1,
p.
105.
Cortez, M. I.
and
Solomyak, B.
2011.
Invariant measures for non-primitive tiling substitutions.
Journal d'Analyse Mathématique,
Vol. 115,
Issue. 1,
p.
293.
PIACQUADIO, MARÍA N.
and
HANSEN, ROBERTA
2011.
MENDÈS FRANCE AND THERMODYNAMICAL SPECTRA: A COMPARATIVE STUDY OF CONTRACTIVE AND EXPANSIVE FRACTAL PROCESSES.
Fractals,
Vol. 19,
Issue. 01,
p.
51.
Aougab, Tarik
Dong, Stella Chuyue
and
Strichartz, Robert
2012.
Laplacians on a family of quadratic Julia sets II.
Communications on Pure and Applied Analysis,
Vol. 12,
Issue. 1,
p.
1.
Strichartz, Robert S.
and
Teplyaev, Alexander
2012.
Spectral analysis on infinite Sierpiński fractafolds.
Journal d'Analyse Mathématique,
Vol. 116,
Issue. 1,
p.
255.
Essouabri, Driss
and
Lichtin, Ben
2013.
Zeta functions of discrete self-similar sets.
Advances in Mathematics,
Vol. 232,
Issue. 1,
p.
142.
BANAKH, T.
and
NOVOSAD, N.
2014.
MICRO AND MACRO FRACTALS GENERATED BY MULTI-VALUED DYNAMICAL SYSTEMS.
Fractals,
Vol. 22,
Issue. 04,
p.
1450012.
 $\left\{ {{T}_{1}},...,{{T}_{m}} \right\}$ on a discrete metric space
$\left\{ {{T}_{1}},...,{{T}_{m}} \right\}$ on a discrete metric space 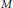 $M$. An invariant set
$M$. An invariant set  $F$ is defined to be a set satisfying
$F$ is defined to be a set satisfying 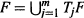 $F\,=\,\bigcup _{j=1}^{m}\,{{T}_{j}}F$, and an invariant measure
$F\,=\,\bigcup _{j=1}^{m}\,{{T}_{j}}F$, and an invariant measure 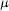 $\mu $ is defined to be a solution of
$\mu $ is defined to be a solution of 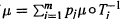 $\mu \,=\,\sum{_{j=1}^{m}\,{{p}_{j}}\mu {}^\circ T_{j}^{-1}}$ for positive weights
$\mu \,=\,\sum{_{j=1}^{m}\,{{p}_{j}}\mu {}^\circ T_{j}^{-1}}$ for positive weights 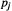 ${{p}_{j}}$. The structure and basic properties of such invariant sets and measures is described, and some examples are given. A blowup
${{p}_{j}}$. The structure and basic properties of such invariant sets and measures is described, and some examples are given. A blowup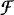 $\mathcal{F}$ of a self-similar set
$\mathcal{F}$ of a self-similar set  $F$ in
$F$ in 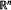 ${{\mathbb{R}}^{n}}$ is defined to be the union of an increasing sequence of sets, each similar to
${{\mathbb{R}}^{n}}$ is defined to be the union of an increasing sequence of sets, each similar to  $F$. We give a general construction of blowups, and show that under certain hypotheses a blowup is the sum set of
$F$. We give a general construction of blowups, and show that under certain hypotheses a blowup is the sum set of  $F$ with an invariant set for a r.i.f.s. Some examples of blowups of familiar fractals are described. If
$F$ with an invariant set for a r.i.f.s. Some examples of blowups of familiar fractals are described. If 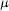 $\mu $ is an invariant measure on
$\mu $ is an invariant measure on 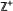 ${{\mathbb{Z}}^{+}}$ for a linear r.i.f.s., we describe the behavior of its analytic transform, the power series
${{\mathbb{Z}}^{+}}$ for a linear r.i.f.s., we describe the behavior of its analytic transform, the power series 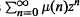 $\sum{_{n=0}^{\infty }\mu (n){{z}^{n}}}$ on the unit disc.
$\sum{_{n=0}^{\infty }\mu (n){{z}^{n}}}$ on the unit disc.

