Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grinberg, Shaul
1985.
On invariant linear functionals.
Indagationes Mathematicae (Proceedings),
Vol. 88,
Issue. 3,
p.
299.


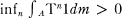 for any measurable subset
for any measurable subset 