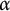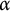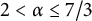The first-order theory of binary overlap-free words is decidable

Abstract

We show that the first-order logical theory of the binary overlap-free words (and, more generally, the $\alpha $-free words for rational $\alpha $, $2 < \alpha \leq 7/3$), is decidable. As a consequence, many results previously obtained about this class through tedious case-based proofs can now be proved “automatically,” using a decision procedure, and new claims can be proved or disproved simply by restating them as logical formulas.

1 Introduction

Let $V_k(n)$ be the highest power of k dividing n; thus, for example, we have $V_2 (48) = 16$ . A famous theorem of Büchi [7], as corrected and clarified by Bruyère et al. [6], states that for each integer $k\geq 2$ , the first-order logical theory $\operatorname {\mathrm {FO}}(\mathbb {N}, +, <, 0, 1, V_k)$ is decidable. (The logical structure $(\mathbb {N}, +, <, 0, 1, V_2)$ is sometimes called Büchi arithmetic; it is an extension of the more familiar Presburger arithmetic.) As a consequence, it follows that the first-order theory of k-automatic sequences is decidable.

Recently decidability results have been proved for a number of interesting infinite classes of infinite sequences. For the paperfolding sequences, see [15]. For a class of Toeplitz words, see [13]. For the Sturmian sequences, see [16].

In this paper, we prove that a similar result holds for the first-order theory of the binary overlap-free words (and, more generally, for $\alpha $ -power-free words for $\alpha $ a rational number with $2<\alpha \leq 7/3$ ). This allows us to prove (in principle), purely mechanically, assertions about the factors of such words, compare different overlap-free words, and quantify over all overlap-free words or appropriate subsets of them.

A version of this decision algorithm has been implemented using Walnut, a theorem-prover originally designed by Mousavi [21, 27], and we have used it to reprove various known results about overlap-free words, and some new ones.

2 Definitions and basic concepts

Let $x = e_{t-1} \cdots e_1 e_0$ be a word over the alphabet $\{0,1,2\}$ . We define $[x]_2 = \sum _{0 \leq i < t} e_i 2^i$ , the value of x when interpreted in base $2$ . The case where the $e_i \in \{0,1\}$ corresponds to the ordinary binary representation of numbers; if the digit $2$ is also allowed, we refer to the extended binary representation. For example, $[210]_2 = [1010]_2 = 10$ .

Let $x = x[0..n-1]$ be a finite word of length n. If $1 \leq p \leq n$ and $x[i]=x[i+p]$ for $0 \leq i < n-p$ , then we say that x has period p. The least period is called the period, and is denoted $\operatorname {\mathrm {per}}(x)$ . The exponent of a nonempty word x is defined to be $|x|/\operatorname {\mathrm {per}}(x)$ . If $\exp (x) = \alpha $ , we say that x is an $\alpha $ -power. For example, the word onion is a ${5 \over 2}$ -power.

The supremum of $\exp (y)$ , taken over all finite nonempty factors y of x, is called the critical exponent of x, and is denoted $\operatorname {\mathrm {ce}}(x)$ . If $\operatorname {\mathrm {ce}}(x) < \alpha $ , we say that x avoids $\alpha $ -powers or that x is $\alpha $ -power-free. If $\operatorname {\mathrm {ce}}(x) \leq \alpha $ , we say that x avoids $\alpha ^+$ -powers or that x is $\alpha ^+$ -power-free. Thus, when we talk about power-freeness, we are using a sort of “extended reals,” under the agreement that $e < e^+ < f$ for all $e<f$ ; this very useful notational convention was apparently introduced by Kobayashi [19, p. 186]. These concepts extend seamlessly to infinite words. A square is a $2$ -power; an example in English is murmur. The order of a square $xx$ is defined to be $|x|$ .

An overlap is a word of the form $axaxa$ , where a is a single letter and x is a possibly empty word. For example, the French word entente is an overlap. If a word has no factor that is an overlap, we say it is overlap-free. Equivalently, a word is overlap-free iff it avoids $2^+$ -powers. Much of what we know about overlap-free words is contained in Thue’s seminal 1912 paper [2, 30]. For more recent advances, see [8, 14, 22, 24, 25, 28].

The most famous infinite binary overlap-free word is

$$\begin{align*}\mathbf{t} = 01101001\ldots, \end{align*}$$

the Thue–Morse sequence. It satisfies the equation $\mathbf {t} = \mu (\mathbf {t})$ , as does its binary complement $\overline {\mathbf {t}}$ , where $\mu $ is the Thue–Morse morphism mapping $0$ to $01$ and $1$ to $10$ .

We write $\mu ^n$ for the n-fold composition of $\mu $ with itself.

A theorem of Restivo and Salemi [25] provides a structural description of finite and infinite binary overlap-free words in terms of the Thue–Morse morphism $\mu $ . This result was extended to all powers $2 < \alpha \leq {7 \over 3}$ in [18], as follows:

Theorem 2.1 Let $S = \{ \epsilon , 0, 1, 00, 11 \}$ . Let $2 < \alpha \leq {7 \over 3}$ be a rational number $(p/q)$ or extended rational $(p/q)^+$ .

1. (a) Suppose w is a finite binary $\alpha $ -free word. Then there exist words

   $$ \begin{align*}x_0, x_1, \ldots, x_n, y_0, y_1, \ldots, y_{n-1} \in S\end{align*} $$

   such that $w = x_0 \mu (x_1) \mu ^2(x_2) \cdots \mu ^n(x_n) \mu ^{n-1}(y_{n-1}) \cdots \mu (y_1) y_0$ .

2. (b) Suppose $\mathbf {w}$ is an infinite binary $\alpha $ -free word. Then there exist infinitely many words $x_0, x_1, \ldots \in S$ such that $\mathbf {w} = x_0 \mu (x_1) \mu ^2(x_2) \kern-1.2pt\cdots\kern-1pt $ , or finitely many words $x_0, x_1, \ldots , x_n \in S$ such that $\mathbf {w} = x_0 \mu (x_1) \mu ^2(x_2) \cdots \mu ^n(x_n) \, \mathbf {t}$ or $\mathbf {w} = x_0 \mu (x_1) \mu ^2(x_2) \cdots \mu ^n(x_n) \, \overline {\mathbf {t}}$ .

Of course, not all sequences of choices of the $x_i$ and $y_i$ result in overlap-free (or $\alpha $ -power-free) words. For example, taking $x_0 = 0$ , $x_1 = 11$ , $y_0 = 1$ gives the word ${0\, \mu (11) \, 1 = 0 \, 10 \, 10 \, 1 = (01)^3}$ (see [4, 8, 9, 17, 23, 26] for more details). We will see how to compute the codes that do give overlap-free words below, in Section 5.1.

3 Decidability for binary overlap-free words

Theorem 2.1 is our basic tool. We code the words $x_i$ and $y_i$ with the following correspondence:

$$ \begin{align*} g(1) &= \epsilon, \\ g(2) &= 0, \\ g(3) &= 1, \\ g(4) &= 00, \\ g(5) &= 11. \end{align*} $$

The finite code $c_0 c_1 \cdots c_t \in \{1,2,3,4,5\}^*$ is understood to specify the finite Restivo word

$$ \begin{align*}R(c_0 c_1 \cdots c_t) = g(c_0) \mu(g(c_1)) \mu^2(g(c_2)) \cdots \mu^t(g(c_t))\end{align*} $$

and the infinite code $c_0 c_1 \cdots \in \{1,2,3,4,5\}^\omega $ is understood to specify the infinite Restivo word

$$ \begin{align*}R(c_0 c_1 \cdots) = g(c_0) \mu(g(c_1)) \mu^2(g(c_2)) \cdots.\end{align*} $$

Thus, the Restivo words correspond to “one-sided” part (a) of Theorem 2.1.

Similarly, the finite codes $c_0 c_1 \cdots c_t, d_0 d_1 \cdots d_{t-1} \in \{1,2,3,4,5\}^*$ are understood to specify the finite Salemi word

$$ \begin{align*} &S(c_0 c_1 \cdots c_t, d_0 d_1 \cdots d_{t-1}) = \\ &g(c_0) \mu(g(c_1)) \mu^2(g(c_2)) \cdots \mu^t(g(c_t)) \mu^{t-1} (g(d_{t-1})) \cdots \mu^1 (g(d_1)) g(d_0). \end{align*} $$

Thus, the Salemi words correspond to the “two-sided” part (b) of Theorem 2.1.

We emphasize that we do not require that Restivo words and Salemi words be overlap-free, only that they are of the form given above with the $c_i, d_i \in S$ .

We prove the following results:

Theorem 3.1 Let $N_{c,d}$ be the structure $(\mathbb {N}, <, +, 0, 1, n \rightarrow V_2(n), n \rightarrow S(c,d)[n] )$ , where we augment Büchi arithmetic by a finitely coded Salemi word $S(c,d)$ . Let $K_{\mathrm {finite}} = \{ N_{c,d} \, : \, c,d \in \{1,2,3,4,5\}^* \}$ . Then the first-order logical theory $\operatorname {\mathrm {FO}}(K_{\mathrm {finite}})$ is decidable.

Theorem 3.2 Let $N^{\prime }_{\mathbf {c}}$ be the structure $(\mathbb {N}, <, +, 0, 1, n \rightarrow V_2(n), n \rightarrow R(\mathbf {c})[n] )$ , where we augment Büchi arithmetic by a Restivo word $R(\mathbf {c})$ with infinite code $\mathbf {c}$ . Let $K_{\mathrm {infinite}} = \{ N^{\prime }_{\mathbf {c}} \, : \, \mathbf {c} \in \{1,2,3,4,5\}^\omega \}$ . Then the first-order logical theory $\operatorname {\mathrm {FO}}(K_{\mathrm {infinite}})$ is decidable.

Proof of Theorems 3.1 and 3.2.

The basic strategy of our decision procedure can be found in the papers of Büchi [7] and Bruyère et al. [6] mentioned previously. Since Büchi arithmetic itself is decidable, and is powerful enough to express the computations of a deterministic finite automaton (DFA) or deterministic finite automaton with output (DFAO), it suffices to construct a DFAO computing $n \rightarrow S(c,d)[n]$ and $n \rightarrow R(\mathbf {c})[n]$ . Here, the automata take the words coding $c, d, \mathbf {c}$ , and n (in binary) in parallel, and compute the nth bit of the corresponding word. We call these the lookup automata. For the Salemi words, we use ordinary finite automata, and for infinite binary words, we use Büchi automata.

We construct the lookup automata in stages. First, we describe how to compute the lookup automaton for the finite Restivo word

$$ \begin{align*}R(c_0 c_1 \cdots c_t) = g(c_0) \mu(g(c_1)) \mu^2(g(c_2)) \cdots \mu^t(g(c_t)) .\end{align*} $$

Given n, our first task is to determine in which factor the index n lies. To achieve this, we observe that $|\mu ^j (g(i))| = 2^j |g(i)| = a \cdot 2^i$ for $i \in \{1,2,3,4,5\}, a \in \{0,1,2\}$ . Defining the morphism h as follows:

$$ \begin{align*} h(1) &= 0, \\ h(2) &=1, \\ h(3) &= 1,\\ h(4) &= 2,\\ h(5) &= 2, \end{align*} $$

we see that $h(i) = |g(i)|$ . If we now interpret $h(c_t \cdots c_1 c_0)$ as a generalized base- $2$ number with the digit set $\{0,1,2\}$ , we see that the nth symbol of $R(c_0 c_1 \cdots c_t) $ is equal to the $(n-k)$ th symbol of $\mu ^i(g(c_i))$ , where

(3.1) $$ \begin{align} [h(c_{i-1} \cdots c_1 c_0)]_2 \leq n < [h(c_i \cdots c_1 c_0)]_2 , \end{align} $$

and $k = [h(c_{i-1} \cdots c_1 c_0)]_2$ . Here, all words are indexed starting at position $0$ . We can find the appropriate i with an existential quantifier that checks the inequalities (3.1).

Since n is given in binary, we need a normalizer that takes as input two strings in parallel, one over the larger digit set $\{0,1,2\}$ and one over the ordinary digit set $\{0,1\}$ , and accepts if they represent the same number when considered in base $2$ . This is done with the automaton in Figure 1. Correctness of this automaton is easily proved by induction on the length of the input, using the fact that state $0$ corresponds to “no carry” and state $1$ corresponds to “carry expected.”

Figure 1: Normalizer for base- $2$ expansions.

The final piece is the observation that the first $2^i$ bits of $\mathbf {t}$ are just $\mu ^i(0)$ , and the first $2^i$ bits of $\overline {\mathbf {t}}$ are $\mu ^i(1)$ . Since a $2$ -state automaton can compute the nth bit of $\mathbf {t}$ (or $\overline {\mathbf {t}}$ ), we can determine the appropriate bit.

Exactly, the same idea works for the infinite Restivo words, except now the code is an infinite word, so we need to use a Büchi automaton in order to process it correctly.

The finite Salemi words are only slightly more complicated. Here, we use the (easily-verified) fact that

$$ \begin{align*}\mu^{t-1} g(d_{t-1}) \cdots \mu^1 (g(d_1)) g(d_0) = w^R,\end{align*} $$

where

$$ \begin{align*}w = \begin{cases} g(d_0) \mu(\overline{g(d_1)}) \mu^2(g(d_2)) \mu^3(\overline{g(d_3)}) \cdots \mu^{t-1} (g(d_{t-1})), & \text{if }t\ \text{odd}; \\ g(d_0) \mu(\overline{g(d_1)}) \mu^2(g(d_2)) \mu^3(\overline{g(d_3)}) \cdots \mu^{t-1} (\overline{g(d_{t-1})}), & \text{if }t\ \text{even}. \end{cases}\end{align*} $$

On input n, we use the lengths of the finite words $g(c_0) \mu (g(c_1)) \mu ^2(g(c_2)) \cdots \mu ^t(g(c_t))$ and $ \mu ^{t-1} g(d_{t-1}) \cdots \mu ^1 (g(d_1)) g(d_0)$ to decide where the nth symbol lies, and then appeal to the lookup automaton for $R(c_0 \cdots c_t)$ , or its modification for w, to compute the appropriate bit.

This completes our sketch of the decision procedure.

For an infinite word $\mathbf {x}$ , we can write first-order formulas asserting that $\mathbf {x}$ has an overlap (resp. has a $p/q$ -power), as follows:

$$ \begin{align*} \exists i,n \ (n\geq 1) \ \wedge\ \forall t \ (t\leq n) \implies \mathbf{x}[i+t]=\mathbf{x}[i+t+n], \\ \exists i,n \ (n\geq 1) \ \wedge\ \forall t \ (qt<(p-q)n) \implies \mathbf{x}[i+t]=\mathbf{x}[i+t+n]. \end{align*} $$

Here, p and q are positive integer constants and an expression like $qt$ is shorthand for $\overbrace {t+t+{\cdot\!\cdot\!\cdot} +t}^{q\ \mathrm {times}}$ .

So, incorporating these two formulas into larger first-order logical formulas asserting that a given code specifies an overlap-free word (or $\alpha $ -free word for rational or extended rational $\alpha $ with $2 < \alpha \leq 7/3$ ), we immediately get the following corollary:

Corollary 3.3 The first-order theory of the overlap-free words (or more generally, $\alpha $ -free words for rational or extended rational $\alpha $ with $2 < \alpha \leq 7/3$ ), is decidable.

4 Implementation

We implemented part of the decision procedure discussed in Section 3 using Walnut, a theorem-prover originally designed by Mousavi [21].

The main part we implemented was for the finite Restivo words. This allows us to solve many (but not all) questions about infinite overlap-free words. The limitation is because Walnut is based on ordinary finite automata and not Büchi automata.

To implement our decision procedure in Walnut, we represent encodings as strings over the alphabet $\{1,2,3,4,5\}$ . Since the encoded binary string might need more binary digits to specify a position within it than the number of symbols in the encoding, we also allow an arbitrary number of trailing zeros in a code.

All numbers are represented in base $2$ , starting with the least significant digit.

Our Walnut solution needs various subautomata, as follows. Most of these are DFA, with the exception of CODE and LOOK, which are DFAO’s.

• • power2: one argument n. True, if n is a power of $2$ and $0$ otherwise.

• • adjacent: two arguments $m, n$ . True, if $m = 2^i$ , $n = 2^{i-1}$ for some $i \geq 1$ , or if $m = 1$ and $n = 0$ .

• • hmorph: two arguments $c,y$ . True, if y represents applying h to the code specified by c.

• • validcode: one argument c. True, if c represents a valid code, that is, a word in $\{ 1,2,3,4,5 \}^*$ followed by $0$ ’s.

• • length: two arguments $c,n$ . True, if n is the length of the binary string encoded by the codes c.

• • prefix: three arguments $a,b,c$ . Both $b,c$ are are extended binary representations, while a is either $0$ or a power of $2$ in ordinary binary representation. The result is true if the word c equals b copied digit-by-digit, up to and including the position specified by the single $1$ in a, and $0$ ’s thereafter.

• • CODE: a DFAO, two arguments $c, n$ . Returns the code in $\{1,2,3,4,5\}$ corresponding to the digit specified by n, a power of $2$ .

• • look1: two arguments $c, n$ . True, if $R(c_0 c_1 \cdots c_{t-1})[n] = 1$ and $0$ otherwise (which includes the case where the index n is out of range).

• • look2: two arguments $c, n$ . True, if the code c is invalid (for example, because it has interior $0$ ’s) or the index n is out of range.

• • LOOK: a DFAO, two arguments $c, n$ . Returns $R(c_0 c_1 \cdots c_{t-1})[n]$ if the index is in range, and $2$ otherwise. Obtained by combining the DFA’s for look1 and look2.

Here is the Walnut code for these. A brief reminder of Walnut’s syntax may be necessary.

• • A and E represent the universal and existential quantifiers, respectively.

• • lsd_k tells Walnut to interpret numbers in base-k, using least-significant-digit first representation.

• • | is logical OR, & is logical AND, => is logical implication, ~ is logical NOT.

• • reg defines a regular expression.

• • def defines an automaton accepting the representation of free variables making the formula true.

In order to construct the automaton look1, which is the most complicated part of our construction, we use the following auxiliary variables:

• • p, the power of $2$ that corresponds to the particular $\mu ^i (g(c_i))$ block that the nth bit falls in.

• • $q= \lfloor p/2 \rfloor $ .

• • l, a number in extended binary representing the lengths of the strings represented by the codes c.

• • g, a number in extended binary where we have canceled from l the bits corresponding to higher powers of $2$ than p.

• • h, a number in extended binary where we have canceled from l the bits corresponding to higher powers of $2$ than q.

• • r, a base- $2$ index giving the start of the block after which n appears.

• • s, a base- $2$ index giving the start of the block where n appears.

• • x, the relative position inside the appropriate block corresponding to the bit n.

Once these are “guessed” with an existential quantifier, we verify them with the appropriate automata and then compute the appropriate bit depending on the particular $c_i$ , as follows:

The resulting DFAO, LOOK, has 17 states, and is described in Table 1.

Table 1: The DFAO LOOK.

Note: The entries in the columns labeled $[{a\atop b}]$ represent the transitions of the automaton $\delta (q,[a,b])$ . The entries in the column labeled $\tau (q)$ are the outputs of each state. The start state is state $0$ .

5 Applications

5.1 Overlap-free words

We can now use this DFAO to obtain a number of results. First, let us find an automaton recognizing all finite words $c_0 \cdots c_{t-1}$ such that $R(c_0 \cdots c_{t-1})$ is overlap-free. This is done as follows:

The resulting automaton is depicted in Figure 2.

Figure 2: Codes for overlap-free sequences.

This automaton essentially accepts all infinite strings $c_0 c_1 c_2 {\cdots}\!$ such that $R(c_0 c_1{\cdots}\!)$ is overlap-free. However, there are some subtleties that arise in interpreting it, due to the nature of our encoding. We describe them now.

When we compare the automaton in Figure 2 to that in [26], we see the following differences. First, the codes are different, and the correspondence is given in Table 2.

Table 2: Correspondence between codes.

Second, the names of states are different, and the correspondence is given in Table 3. Notice that the automaton in Figure 2 has three additional states, numbered 5,6,9, that do not appear in the automaton given in [26]. The explanation for this is as follows: the only accepting paths from these states end in an infinite tail of $1$ ’s. These paths can only correspond to either a suffix of $\mathbf {t}$ or $\overline {\mathbf {t}}$ , and in all cases the resulting words have overlaps. Therefore, we can delete these states 5,6,9 from Figure 2 and obtain the automaton given in [26].

Table 3: Correspondence between state names.

We now use our automaton for overlap-free words to prove a result, about the lexicographically least overlap-free infinite word, previously proved in [1].

Theorem 5.1 The lexicographically least overlap-free infinite word is $001001 \overline {\mathbf {t}}$ .

Proof We create a Walnut formula that recognizes all finite code strings c with the property that the overlap-free word w specified by c is lexicographically $\leq $ all overlap-free words $w'$ with $|w'| \geq |w|$ . This can be done as follows:

The resulting automaton is depicted in Figure 3. This was a rather big computation in Walnut; the automaton for agrees has 122 states, and required 120GB of RAM and 87,762,417 ms to compute. The largest intermediate automaton had 3,534,633 states.

Figure 3: Codes for lexicographically smallest words.

By inspection of this automaton, we see that the only arbitrarily long accepting path that does not end in $1$ ’s is $4131^*3$ . This corresponds to the word $001001\overline {\mathbf {t}}$ .

Remark 5.2 Using our technique, we can also prove that the same word $001001\overline {\mathbf {t}}$ is the lexicographically least $7/3$ -power-free word, and and hence it is lexicographically least for all $\alpha $ -power-free words with $2< \alpha \leq 7/3$ .

Now, we turn to the following theorem from [5]:

Theorem 5.3 Take the Thue–Morse word $\mathbf {t}$ and flip any finite nonzero number of bits, sending $0$ to $1$ and vice versa. Then the resulting word has an overlap.

At first glance this theorem does not seem susceptible to our technique, because specifying an arbitrary finite set of positions to change requires second-order logic. But we can still prove it! Rather than quantifying over all finite sets of positions to change, we instead quantify over all infinite overlap-free words, and ask for which codes $c_0 c_1 c_2 \cdots $ the specified word agrees with Thue–Morse on an infinite suffix.

If we had implemented our decision procedure for infinite Restivo words using Büchi automata instead of ordinary finite automata, this would be easy to translate into a first-order logical formula. However, the fact that our implementation can only deal with finite codes $c_0 c_1 \cdots c_t$ makes it somewhat harder.

Proof Instead, we use the following idea: we design an automaton to accept all finite codes $c_0 \cdots c_t$ with the property that there exist arbitrarily long finite codes $d_0 \cdots d_s$ such that:

• • $c_0 \cdots c_t$ is a prefix of $d_0 \cdots d_s$ ;

• • $w = R(d_0 \cdots d_s)$ is overlap-free;

• • $|R(c_0 \cdots c_t)| = l$ ;

• • w agrees with $\mathbf {t}$ on the positions from index l to index $|w|-1$ .

This is done with the following Walnut code:

The resulting automaton only accepts $1^*$ , so there are no such codes except that specifying the Thue–Morse sequence.

5.2 ${7\over 3}$ -power-free words

We now apply the method to re-derive the automaton given in [23] for ${7\over 3}$ -power-free words.

This produces, in a purely mechanical fashion, the automaton in Figure 2 of [23] that was previously constructed using a rather tedious examination of cases. The relationship between the old version in that paper and the new version given here is summarized in Table 4.

Table 4: Correspondence between old and new states.

Once again there is a state, state 13, that appears in Figure 4 but not in the paper [23]. Again, this is because the only accepting path reachable from this state consists of an infinite tail of $1$ ’s, which does not result in a ${7 \over 3}$ -power-free word.

Figure 4: Codes for ${7\over 3}$ -power-free sequences.

As an application, let us reprove a result from [11]:

Theorem 5.4 There exist uncountably many infinite ${7\over 3}$ -power-free binary words, each containing arbitrarily large overlaps.

Figure 5: Large overlaps in a ${7\over 3}$ -power-free word.

Proof We claim that every code in $212 \{12,1112\}^i $ corresponds to a ${7\over 3}$ -power-free word with overlaps of i different lengths. The automaton in Figure 4 clearly accepts every word in $212\{12,1112\}^*$ , so the words are ${7\over 3}$ -power-free. To check the property of containing arbitrarily large overlaps, we create an automaton that recognizes, in parallel, those codes in $(211^*)^*2$ , together with the lengths of overlaps that occur in the resulting word.

Inspection of the automaton in Figure 5 proves the claim. Hence, every word coded by $212 \{12,1112\}^\omega $ has overlaps of infinitely many different lengths.

5.3 New results

We can use the framework so far to prove a number of new results about overlap-free and Restivo words.

For example, it is an easy consequence of the Restivo–Salemi theorem that every infinite overlap-free binary word contains arbitrarily large squares. We can prove this—and more—in a quantitative sense.

Theorem 5.5 Every finite overlap-free word of length $l>7$ contains a square of order $\geq l/6$ . Furthermore, the bound is best possible, in the sense that there are arbitrarily large overlap-free words for which the largest square is of order exactly $l/6$ .

Proof We can check the first claim with Walnut as follows:

Figure 6: Codes for length-l overlap-free words with largest square of order $l/6$ .

For the second claim, we can actually determine all code sequences for which the largest square is of order exactly $l/6$ .

The resulting automaton is depicted in Figure 6.

In particular, the code sequence $4(32)^i13$ has length $6 \cdot 4^i$ and has largest square of order $4^i$ .

We can prove a similar, but weaker bound, for the larger class of all Restivo words:

Theorem 5.6 Every finite Restivo word of length $l>8$ contains a square of order $\geq (l+2)/7$ . Furthermore, the bound is best possible, in the sense that there are arbitrarily large overlap-free words for which the largest square is of order exactly $(l+2)/7$ .

Proof For the first statement, we use

which evaluates to TRUE.

Figure 7: Codes for length-l Restivo words with largest square of order $(l+2)/7$ .

For the second, we construct an automaton accepting those code sequences c for which the largest square is of order exactly $(l+2)/7$ .

The resulting automaton is depicted in Figure 7.

As you can see, code words of the form $5^i 312$ achieve the bound.

As we have seen, not all code sequences result in overlap-free or ${7\over 3}$ -power-free words. If we consider all code sequences, however, then we can prove the following new result:

Theorem 5.7

1. (a) Every (one-sided right) infinite word coded by a member of $\{1,2,3,4,5\}^\omega $ is $4$ th-power-free.

2. (b) Furthermore, this bound is best possible, in the sense that for each exponent $e < 4$ there is an infinite word coded by a code in $\{1,2,3,4,5\}^\omega $ having a critical exponent $>e$ .

Proof

1. (a) We can check this with Walnut as follows:

   

   This asserts the existence of a $4$ th power, and returns FALSE, so no fourth power exists.

2. (b) This requires a little more work. What we do is show that for all finite codes of length $t \geq 3$ , there is a code resulting in a word having a factor of length $2^t-1$ with period $2^{t-2}$ , and hence an exponent of $4(1 - 2^{-t})$ .

   

   Figure 8: Codes for words of critical exponent close to $4$ .

   

   The resulting automaton is depicted in Figure 8.

   From this, we see that the codes of length t specifying a word with critical exponent at least $4(1-2^{-t})$ are

   $$ \begin{align*}2^{t-2}5\{3,5\}, 3^{t-2}4\{2,4\}, 42^{t-3}5\{3,5\}, 53^{t-3}4\{2,4\}.\end{align*} $$

6 Enumeration

As discussed in several previous papers (e.g., [10, 12]), the automaton-based technique can also be used to enumerate, not simply decide, certain aspects of sequences.

Here, we will use these ideas to enumerate the “irreducibly extensible words” of Kobayashi [20]: these are binary words x such that there exists an infinite binary word $\mathbf {y}$ such that $x\mathbf {y}$ is overlap-free. For example, it is easily checked that $010011001011010010$ is extendable, but $010011001011010011$ is not (every extension by a word of length $7$ gives an overlap). Denote the number of such words as $E(n)$ . Table 5 gives the first few values of this sequence.

Table 5: First few values of $E(n)$ .

This is sequence A356959 in the On-Line Encyclopedia of Integer Sequences [29].

We can now obtain the following result of Kobayashi [20]:

Theorem 6.1 $E(n) = \Theta (n^\beta )$ , for $\beta \doteq 1.15501186367066470321$ .

Proof In order to carry out the enumeration, we need to create a first-order logical formula asserting that c is a code for an overlap-free sequence of length at least n, and also that c is lexicographically first with this property in some appropriate order. The easiest lexicographic order results from interpreting c as a number in base $6$ . Then, counting the number of such codes corresponding to each n gives $E(n)$ . We can carry this out with the following Walnut code:

Here, Walnut returns a so-called linear representation for $E(n)$ : this consists of a row vector v, a matrix-valued morphism $\gamma $ , and a column vector w such that $E(n) = v \gamma (x) w$ if x is a binary word with $[x]_2 = n$ . (For more about linear representations, see the book [3].) The rank of a linear representation is the dimension of the vector v; in this case, it is $57$ . With this linear representation in hand, we can compute $E(n)$ very rapidly even for large n.

The linear representation also can give us information about the asymptotic behavior of $E(n)$ . To do so, it suffices to compute the minimal polynomial of the matrix $\gamma (0)$ with a computer algebra system such as Maple; it is

$$ \begin{align*}X^4 (X^4-2X^3-X^2+2X-2)(X-1)^2(X+1)^2.\end{align*} $$

Here, the dominant zero is that of $X^4-2X^3-X^2+2X-2$ , and it is

$$ \begin{align*}\zeta = {{1+ \sqrt{5 + 4 \sqrt{3}}}\over 2} \doteq 2.22686154846556164.\end{align*} $$

It follows that $E(2^n) \sim \alpha \cdot \zeta ^n$ for some constant $\alpha $ ; since E is strictly increasing, it follows that $E(n) = \Theta (n^\beta )$ for $\beta = \log _2(\zeta ) \doteq 1.15501186367066470321$ .

7 Going further

All the needed Walnut code can be downloaded from the website of the second author, https://cs.uwaterloo.ca/~shallit/walnut.html.

In principle, one can extend this work to the Salemi words, and we were able to construct the needed lookup automaton, which has 124 states. However, so far we have been unable to use it to do much that is useful with it, because of the very large sizes of the intermediate automata (at least hundreds of millions of states). We leave this as a problem for future work.