Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T18:53:46.175Z Has data issue: false hasContentIssue false
  • English
  • Français

A First Approximation to {X, Y}

Published online by Cambridge University Press:  20 November 2018

Benson Samuel Brown
Benson Samuel Brown*
Affiliation:
Sir George Williams University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If ℭ and ℭ′ are classes of finite abelian groups, we write ℭ + ℭ′ for the smallest class containing the groups of ℭ and of ℭ′. For any positive number r, ℭ < r is the smallest class of abelian groups which contains the groups Zp for all primes p less than r.

Our aim in this paper is to prove the following theorem.

THEOREM. Iƒ ℭ is a class of finite abelian groups and

(i) πi(Y) ∈ℭ for i < n,

(ii) H*(X; Z) is finitely generated,

(iii) Hi(X;Z)∈ ℭ for i > n + k,

Then

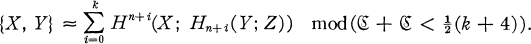
This statement contains many of the classical results of homotopy theory: the Hurewicz and Hopf theorems, Serre's (mod ℭ) version of these theorems, and Eilenberg's classification theorem. In fact, these are all contained in the case k = 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 702 - 711
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Adams, J. F., Stable homotopy theory, Notes by Vasquez, A. T., University of California, Berkeley, 1961; lecture notes in mathematics, no. 3 (Springer-Verlag, Berlin, 1964).Google Scholar
2. Adem, J., The relations on Steenrod powers of cohomology classes, ﹛Algebraic geometry and topology), A symposium in honor of S. Lefschetz, pp. 191–238 (Princeton Univ. Press, Princeton, N.J., 1957).Google Scholar
3. Barcus, W. D. and Meyer, J.-P., The suspension of a loop space, Amer. J. Math. 80 (1958), 895–920.Google Scholar
4. Brown, B. S., The mod e suspension theorem, Can. J. Math. 21 (1969), 684–701.Google Scholar
5. Cartan, H., Algebres d'Eilenberg-MacLane et homotopie, Séminaire Henri Cartan, 1954-1955 (Secrétariat mathématique, 1956).Google Scholar
6. Eckmann, B. and Hilton, P. J., Décomposition homologique d'un polyèdre simplement connexe, C. R. Acad. Sci. Paris 248 (1959), 2054–2056.Google Scholar
7. Eilenberg, S. and MacLane, S., Relations between homology and homotopy groups of spaces, Ann. of Math. (2) 46 (1945), 480–509.Google Scholar
8. Hu, S.-T., Homotopy theory, Pure and Applied Mathematics, Vol. VIII (Academic Press, New York, 1959).Google Scholar
9. Moore, J. C., On homotopy groups of spaces with a single non-vanishing homology group, Ann. of Math. (2) 59 (1954), 549–557.Google Scholar
10. Serre, J.-P., Homologie singulière des espaces fibres. Applications, Ann. of Math. (2) 54 (1951), 425–505.Google Scholar
11. Serre, J.-P., Groupes d1 homotopie et classes de groupes abêliens, Ann. of Math. (2) 58 (1953), 258–294.Google Scholar
12. Serre, J.-P., Cohomologie modulo 2 des complexes d'Eilenberg-MacLane, Comment. Math. Helv. 27 (1953), 198–232.Google Scholar
13. Spanier, E. H., Duality and the suspension category, International Symposium on Algebraic Topology, Symposium Internacional de Topologia Algebrica, 1956 (Universidad Nacional Atonoma de Mexico, UNESCO, 1958).Google Scholar
14. Thomas, P. E., “A spectral sequence for i£-theory”, Appendix in Lectures on K﹛X) by Bott, R. H., Harvard University, 1962.Google Scholar
15. Toda, H., p-primary components of homotopy groups. II. mod p Hopf invariant, Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 81 (1958), 143–160.Google Scholar
16. Toda, H., p-primary components of homotopy groups. IV. Compositions and toric constructions, Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 32 (1959), 297–332 Google Scholar