Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T17:15:55.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Nets, I. Numerical Invariants

Published online by Cambridge University Press:  20 November 2018

R. H. Bruck
R. H. Bruck*
Affiliation:
University of Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

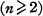A finite net N of degree k, order n, is a geometrical object of which the precise definition will be given in §1. The geometrical language of the paper proves convenient, but other terminologies are perhaps more familiar. A finite affine (or Euclidean) plane with n points on each line is simply a net of degree n+ 1, order n (Marshall Hall [1]). A loop of order n is essentially a net of degree 3, order n (Baer [1], Bates [1]). More generally, for , a set of k —2 mutually orthogonal n ⨯ n latin squares may be used to define a net of degree k, order n (and conversely) by paralleling Bose's correspondence (Bose [1]) between affine planes and complete sets of orthogonal latin squares.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 3 , 1951 , pp. 94 - 107
Copyright
Copyright © Canadian Mathematical Society 1951

References

[1] A. A. Albert, Quasigroups I, Trans. Amer. Soc, vol. 54 (1943), 502-519; Quasigroups II, loc. cit., vol. 55 (1944), 401–419.Google Scholar
[1] Baer, Reinhold Nets and groups, Trans. Amer. Math. Soc, vol. 46 (1939), 110-141; Nets and groups. II, loc. cit., vol. 47 (1940), 435–439.Google Scholar
[2] Baer, Reinhold The homomorphism theorems for loops, Amer. J. Math., vol. 67 (1945), 450–460.Google Scholar
[1] Bateman, P. T. A remark on infinite groups, Amer. Math. Monthly, vol. 57 (1950), 623–624.Google Scholar
[1] Bates, Grace E. Free loops and nets and their generalizations, Amer. J. Math., vol. 69 (1947), 499–550 .Google Scholar
[1] Bol, G. Geweben und Gruppen, Math. Ann., vol. 114 (1937), 414–431.Google Scholar
[1] Bose, R. C. On the application of the properties of Galois fields to the problem of construction of hyper- Graeco-latin squares, Sankya, Indian Journal of Statistics, vol. 3 (1938), 323–338.Google Scholar
[1] Bose, R. C. and Nair, K. R. On complete sets of latin squares, Sankya, vol. 5 (1942), 361–382.Google Scholar
[1] Bruck, R. H. Contributions to the theory of loops, Trans. Amer. Math. Soc, vol. 60 (1946), 245–354.Google Scholar
[1] Bruck, R. H. and Ryser, H. J. The non-existence of certain finite projective planes, Can. J. Math., vol. 1 (1949), 88–93.Google Scholar
[1] Euler, L. Recherches sur une nouvelle espèce quarrés magiques, Collected works, series prima, vol. 7, 291–392.Google Scholar
[1] Fisher, R. A. and Yates, F. The 6 ⨯ 6 latin squares, Proc Camb. Phil. Soc, vol. 30 (1934), 492–507.Google Scholar
[2] Fisher, R. A. and Yates, F. Statistical tables for agricultural, biological and medical research (Edinburgh, 1943.)Google Scholar
[1] Hall, Marshall Projective planes, Trans. Amer. Math. Soc, vol. 54 (1943), 29–77.Google Scholar
[1] Kendali, M. G. Who discovered the latin square?, American Statistician, vol. 2 (1948), 13.Google Scholar
[1] Levi, F. W. Finite geometrical systems (University of Calcutta, 1942.)Google Scholar
[1] MacDuffee, C. C. The theory of matrices (New York, 1946.)Google Scholar
[1] MacNeish, H. F. Euler squares, Ann. of Math., vol. 23 (1921-2), 221–227.Google Scholar
[1] Mann, H. B. The construction of orthogonal squares, Ann. of Math. Statistics, vol. 13 (1942), 418–423.Google Scholar
[2] Mann, H. B. On orthogonal latin squares, Bull. Amer. Math. Soc, vol. 50 (1944), 249–257.Google Scholar
[3] Mann, H. B. Analysis and design of experiments (New York, 1949.)Google Scholar
[1] Norton, H. W. The 7 ⨯ 7 squares, Ann. Eugen., vol. 9 (1939), 269–307.Google Scholar
[1] Paige, L. J. A note on finite abelian groups, Bull. Amer. Math. Soc, vol. 53 (1947), 590–593.Google Scholar
[2] Norton, H. W. Neofields, Duke Math. J., vol. 16 (1949), 39–60.Google Scholar
[1] Sade, Albert Enumération des carrés latins. Application au 7e ordre. Conjecture pour les ordres supérieurs. (Published by the author, Marseille, 1948.)Google Scholar
[1] Stevens, W. L. The completely orthogonalized latin square, Ann. Eugen., vol. 9(1939), 82–93.Google Scholar
[1] Tarry, G. Le probléme de 36 officiers, Compte Rendu de l'Association Franç aise pour l'Avancement de Science Naturel, vol. 1 (1900), 122-123; vol. 2 (1901), 170–203.Google Scholar