Article contents
Federer-Čech Couples
Published online by Cambridge University Press: 20 November 2018
Extract
In (5),I considered two-term conditions in π-exact couples, of which the exact couple 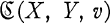 of Federer (7) is an example. Let M(X, Y)be the space of all maps from X to Y with the compact-open topology. Our aim in this paper is to construct a π-exact couple
of Federer (7) is an example. Let M(X, Y)be the space of all maps from X to Y with the compact-open topology. Our aim in this paper is to construct a π-exact couple 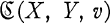 , where Xis a finite-dimensional (in the sense of Lebesgue) metric space and
, where Xis a finite-dimensional (in the sense of Lebesgue) metric space and 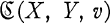 , a certain (rather large) class of spaces. Specifically,
, a certain (rather large) class of spaces. Specifically, 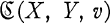 is the class of all topological spaces Xwhich possess the following property (P).
is the class of all topological spaces Xwhich possess the following property (P).
(P) Let Y be a (possibly infinite) simplicial complex. There exists x0 ∈ X and y0 ∊ Y such that [X, x0]≃ [Y, y0].
In § 5 it will be seen that 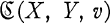 contains all CW complexes and all metric absolute neighbourhood retracts (ANR)s.
contains all CW complexes and all metric absolute neighbourhood retracts (ANR)s.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
References
- 1
- Cited by


