Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-03T20:21:23.339Z Has data issue: false hasContentIssue false
  • English
  • Français

The Family of Lodato Proximities Compatible With a Given Topological Space

Published online by Cambridge University Press:  20 November 2018

W. J. Thron  and
R. H. Warren
W. J. Thron
Affiliation:
University of Colorado, Boulder, Colorado
R. H. Warren
Affiliation:
Aerospace Research Laboratories, Wright-Patterson AFB, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, 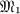) be a topological space. By 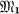we denote the family of all Lodato proximities on X which induce 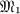. We show that 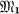is a complete distributive lattice under set inclusion as ordering. Greatest lower bound and least upper bound are characterized. A number of techniques for constructing elements of 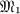are developed. By means of one of these constructions, all covers of any member of 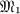can be obtained. Several examples are given which relate 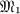to the lattice 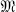of all compatible proximities of Čech and the family 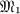of all compatible proximities of Efremovič. The paper concludes with a chart which summarizes many of the structural properties of 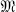, 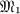and .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 2 , April 1974 , pp. 388 - 404
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Birkhoff, G., Lattice theory, Amer. Math. Soc. Colloq. Pub. Vol. 25, third edition (Amer. Math. Soc, Providence, 1967).Google Scholar
2. Davis, A. S., Indexed systems of neighborhoods for general topological spaces, Amer. Math. Monthly 68 (1961), 886–893.Google Scholar
3. Dooher, T. E. and Thron, W. J., Proximities compatible with a given topology, Dissertationes Math. Rozprawy Mat. 71 (1970), 1–38.Google Scholar
4. Dooher, T. E. and Warren, R. H., Structure of the set of compatible proximities when the set is finite (communicated).Google Scholar
5. Lodato, M. W., On topologically induced generalized proximity relations, Proc. Amer. Math. Soc. 15 (1964), 417–422.Google Scholar
6. Lodato, M. W., On topologically induced generalized proximity relations, II, Pacific J. Math. 17 (1966), 131–135.Google Scholar
7. Mozzochi, C. J., Gagrat, M. S., and Naimpally, S. A., Symmetric generalized topological structures, available from the authors (Mozzochi, Yale Univ., New Haven, CT; Gagrat, Indian Institute of Technology, Kanpur, India; Naimpally, Lakehead Univ., Thunder Bay, Canada), mimeographed (1969).Google Scholar
8. Naimpally, S. A. and Warrack, B. D., Proximity spaces (Cambridge University Press, London, 1970). Google Scholar
9. Sharma, P. L. and Naimpally, S. A., Construction of Lodato proximities, Math. Japon. 15 (1970), 101–103.Google Scholar
10. Thron, W. J., Topological structures (Holt, Rinehart and Winston, New York, 1966).Google Scholar
11. Thron, W. J. and Warren, R. H., On the lattice of proximities of Cech compatible with a given closure space, Pacific J. Math, (to appear).Google Scholar