Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T23:19:43.448Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Problems for Functions Starlike in the Exterior of the Unit Circle

Published online by Cambridge University Press:  20 November 2018

W. C. Royster
W. C. Royster*
Affiliation:
University of Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Σ represent the class of analytic functions

(1)

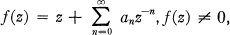
which are regular, except for a simple pole at infinity, and univalent in |z| > 1 and map |z| > 1 onto a domain whose complement is starlike with respect to the origin. Further let Σ- 1 be the class of inverse functions of Σ which at w = ∞ have the expansion

(2).

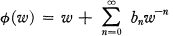In this paper we develop variational formulas for functions of the classes Σ and Σ- 1 and obtain certain properties of functions that extremalize some rather general functionals pertaining to these classes. In particular, we obtain precise upper bounds for |b2| and |b3|. Precise upper bounds for |b1|, |b2| and |b3| are given by Springer (8) for the general univalent case, provided b0 =0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 540 - 551
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Garabedian, P. R. and Schiffer, M., Identities in the theory of conformai mapping, Trans. Amer. Math. Soc, 65 (1949), 187–238.Google Scholar
2. Goodman, A. W., The rotation theorem for starlike univalent functions, Proc. Amer. Math. Soc, 4 (1953), 278–286.Google Scholar
3. Hummel, J. A., A variational method for starlike functions, Proc. Amer. Math. Soc, 9 (1958), 82–87.Google Scholar
4. Hummel, J. A., Extremal problems in the class of starlike functions, Proc. Amer. Math. Soc, 11 (1960), 741–749.Google Scholar
5. Julia, G., Sur une équation aux dérivées fonctionelles, Ann. Ecole Norm., 89 (1922), 1–28.Google Scholar
6. Schiffer, M., Applications of variational methods in the theory of conformai mapping, Proceedings of the Symposia in Applied Mathematics, 1956.Google Scholar
7. Schiffer, M., Faber polynomials in the theory of univalent function, Bull. Amer. Math. Soc, 54 (1948), 503–517.Google Scholar
8. Springer, G., The coefficient problem for schlicht mappings of the exterior of the unit circle, Trans. Amer. Math. Soc, 70 (1951), 421–450.Google Scholar
9. Zamorski, J., Differential equations for the extremal starlike functions, Ann. Pol. Math., 7 (1960), 279–283.Google Scholar