Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T08:10:50.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Metric for the First Eigenvalue on a Klein Bottle

Published online by Cambridge University Press:  20 November 2018

Dmitry Jakobson ,
Nikolai Nadirashvili  and
Iosif Polterovich
Dmitry Jakobson
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke St. West, Montréal QC, H3A 2K6 e-mail: [email protected]
Nikolai Nadirashvili
Affiliation:
Department of Mathematics, University of Chicago, 5734 University Avenue, Chicago, IL 60637, U.S.A. e-mail: [email protected]
Iosif Polterovich
Affiliation:
Département de Mathématiques et de Statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal QC, H3C 3J7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first eigenvalue of the Laplacian on a surface can be viewed as a functional on the space of Riemannian metrics of a given area. Critical points of this functional are called extremal metrics. The only known extremal metrics are a round sphere, a standard projective plane, a Clifford torus and an equilateral torus. We construct an extremal metric on a Klein bottle. 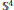It is a metric of revolution, admitting a minimal isometric embedding into a sphere ${{\mathbb{S}}^{4}}$ by the first eigenfunctions. Also, this Klein bottle is a bipolar surface for Lawson's 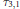${{\tau }_{3,1}}$-torus. We conjecture that an extremal metric for the first eigenvalue on a Klein bottle is unique, and hence it provides a sharp upper bound for 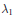${{\lambda }_{1}}$ on a Klein bottle of a given area. We present numerical evidence and prove the first results towards this conjecture.

Keywords

58J5053C42LaplacianeigenvalueKlein bottle
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 2 , 01 April 2006 , pp. 381 - 400
Copyright
Copyright © Canadian Mathematical Society 2006

References

[BeL] Beeckmann, B., Lökes, H., Estimates for the eigenvalues of Hill's equation and applications for the eigenvalues of the Laplacian on toroidal surfaces. Manuscripta Math. 68(1990), no. 3, 295–308.Google Scholar
[B] Berger, M., Sur les premières valeurs propres des variétés riemanniennes. Compositio Math. 26(1973), 129–149.Google Scholar
[CL] Coddington, E. A. and Levinson, N., Theory of ordinary differential equations. McGraw-Hill, New York, 1955.Google Scholar
[EGJ] El Soufi, A., Giacomini, H., and Jazar, M.. Greatest least eigenvalue of the Laplacian on the Klein bottle. Preprint math.MG/0506585.Google Scholar
[EI1] El Soufi, A. and Ilias, S., Immersions minimales, première valeur propre du laplacien et volume conforme. Math. Ann. 275(1986), no. 2, 257–267.Google Scholar
[EI2] El Soufi, A. and Ilias, S., Riemannian manifolds admitting isometric immersions by their first eigenfunctions. Pacific J. Math. 195(2000), no. 1, 91–99.Google Scholar
[EI3] El Soufi, A. and Ilias, S., Critical metrics of the trace of the heat kernel on a compact manifold. J. Math. Pures Appl. 81(2002), no. 10, 1053–1070.Google Scholar
[Erd] Erdlyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G. eds. Higher transcendental functions. Vol. 2, McGraw-Hill, 1953.Google Scholar
[FP] Ferus, D. and Pedit, F., S1-equivariant minimal tori in S 4 and S 1 -equivariant Willmore tori in S 3 . Math. Z. 204(1990), no. 2, 269–282.Google Scholar
[H] Hersch, J., Quatre propriétés isopérimétriques de membranes sphérique homogènes. C. R. Acad. Paris Sér A-B 270(1970), A1645–A1648.Google Scholar
[HL] Hsiang, W-Y. and Lawson, H. B., Minimal submanifolds of low cohomogeneity. J. Differential Geom. 5(1971), 1–38.Google Scholar
[Ken] Kenmotsu, K., A characterization of bipolar minimal surfaces in S 4 . Tôhoku Math. J. 26(1974), 587–598.Google Scholar
[L] Lawson, H. B. Complete minimal surfaces in S 3 . Ann. of Math. 92(1970), 335–374.Google Scholar
[LY] Li, P. and Yau, S.-T., A new conformal invariant and its applications to the Willmore conjecture and the first eigenvalue of compact surfaces. Invent.Math. 69(1982), no. 2, 269–291.Google Scholar
[MR] Montiel, S. and Ros, A., Minimal immersions of surfaces by the first eigenfunctions and conformal area. Invent. Math. 83(1985), no. 1, 153–166.Google Scholar
[N1] Nadirashvili, N., Berger's isoperimetric problem and minimal immersions of surfaces. Geom. Funct. Anal. 6(1996), 877–897.Google Scholar
[N2] Nadirashvili, N., Multiple eigenvalues of the Laplace operator. Mat. Sb. (N.S.) 133(175)(1987), no. 2, 223–237, 272.Google Scholar
[SY] Schoen, R. and Yau, S.-T., Lectures on Differential Geometry. International Press, Cambridge, MA, 1994.Google Scholar
[U] Uhlenbeck, K., Equivariant harmonic maps into spheres. In Harmonic maps (New Orleans, La., 1980), In: HarmonicMaps. Lecture Notes in Math. 949, Springer, Berlin, 1982, pp. 146–158.Google Scholar
[WW] Whittaker, E. T., Watson, G. N., A course in modern analysis, Fifth edition. Cambridge University Press, New York, 1969.Google Scholar
[YY] Yang, P., Yau, S.-T., Eigenvalues of the Laplacian of compact Riemann surfaces and minimal submanifolds. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 7(1980), no. 1, 55–63.Google Scholar