Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T14:31:56.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Exterior Univalent Harmonic Mappings With Finite Blaschke Dilatations

Published online by Cambridge University Press:  20 November 2018

D. Bshouty  and
W. Hengartner
D. Bshouty
Affiliation:
Department of Mathematics, Technion, Haifa, Israel email: [email protected]
W. Hengartner
Affiliation:
D´epartement des Mathématiques, Université Laval, Laval, Québec email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we characterize the univalent harmonic mappings from the exterior of the unit disk, 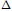$\Delta $, onto a simply connected domain 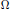$\Omega $ containing infinity and which are solutions of the system of elliptic partial differential equations 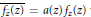$\overline{{{f}_{{\bar{z}}}}\left( Z \right)}=a\left( z \right){{f}_{z}}\left( z \right)$ where the second dilatation function 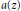$a\left( z \right)$ is a finite Blaschke product. At the end of this article, we apply our results to nonparametric minimal surfaces having the property that the image of its Gauss map is the upper half-sphere covered once or twice.

Keywords

30C5530C6249Q05harmonic mappingsminimal surfaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 470 - 487
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Bshouty, D. and Hengartner, W., Boundary values versus dilatations of harmonic mappings. J. Analyse Math. 72 (1997), 141–164.Google Scholar
[2] Hengartner, W. and Schober, G., Harmonic mappings with given dilatation. J. London Math. Soc.. (2) 33 (1986), 473–483.Google Scholar
[3] Hengartner, W. and Schober, G., Univalent harmonic exterior and ring mappings. J. Math. Anal. Appl. (1) 156 (1991), 154–171.Google Scholar
[4] Pommerenke, C., Boundary Behaviour of Conformal Maps. Grundlehren Math. Wiss. 299, 1991, Springer Verlag.Google Scholar