Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T05:28:43.047Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of Certain Maps to Automorphisms of m

Published online by Cambridge University Press:  20 November 2018

I. D. Berg
I. D. Berg*
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider Banach space automorphisms of m, the space of bounded sequences, which map c, the space of convergent sequences, into itself. In particular, we consider the problem of determining which maps from C0, the space of sequences converging to 0, to c can be extended to such automorphisms.

The origin of this note lies in an incorrect conjecture of mine. If the automorphism T: m → m is given by a matrix, that is, a sequence of elements of ll, and if T is conservative, that is, T(c) ⊂ c, then T(c) = c. That is, T restricted to c is an automorphism of c. We had hoped this would hold even if T were not a matrix. We can see, for example, that if the conservative automorphism T is bounded on the unit cube of m by 1 and ρ, where 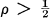, then T(c) = c. However, in general it is possible for a conservative automorphism of m to map c properly into c.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 308 - 316
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Cambern, M., On isomorphisms with small bounds, Proc. Amer. Math. Soc. 18 (1967), 1062–1066.Google Scholar
2. Day, M. M., Normed linear spaces (Springer-Verlag, Berlin, 1962).Google Scholar
3. Lindenstrauss, J. and Rosenthal, H. P., Automorphisms in CQ, I, and m, Israel J. Math. 7 (1969), 227–239.Google Scholar
4. Wilansky, A., Topological divisors of zero and Tauberian theorems, Trans. Amer. Math. Soc. 113 (1964), 240–251.Google Scholar