Article contents
Extending Algebras to Model Congruence Schemes
Published online by Cambridge University Press: 20 November 2018
Extract
This paper is concerned with the description of principal congruence relations. Given elements a and b of a universal algebra 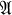 , let θ(a, b) denote the smallest congruence relation on
, let θ(a, b) denote the smallest congruence relation on 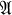 containing the pair 〈a, b〉. One of the earliest characterizations of θ(a, b) is Mal'cev's well-known result [5, Theorem 1.10.3], which says that c ≡ d(θ(a, b)) if and only if there exists a sequence z0, z1, …, zn of elements of
containing the pair 〈a, b〉. One of the earliest characterizations of θ(a, b) is Mal'cev's well-known result [5, Theorem 1.10.3], which says that c ≡ d(θ(a, b)) if and only if there exists a sequence z0, z1, …, zn of elements of 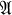 and a sequence f1, f2, …, fn of unary algebraic functions such that c = z0, d = zn, and for each i = 1, …, n,
and a sequence f1, f2, …, fn of unary algebraic functions such that c = z0, d = zn, and for each i = 1, …, n,
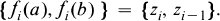
Although this describes θ(a, b) in terms of a set of unary algebraic functions, it is not possible to predict the number or complexity of the unary functions used independently of the choice of a, b, c and d. Several recent papers ([1], [2], [3], [4], [6]) investigate classes of algebras in which principal congruences are simpler.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
- 1
- Cited by


