Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T09:45:15.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Weak Solutions of Linear Subelliptic Dirichlet Problems with Rough Coefficients

Published online by Cambridge University Press:  20 November 2018

Scott Rodney
Scott Rodney*
Affiliation:
Cape Breton University, Nova Scotia email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article gives an existence theory for weak solutions of second order non-elliptic linear Dirichlet problems of the form

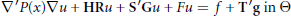$${\nabla }'P\left( x \right)\nabla u+\text{HR}u+\text{{S}'G}u\text{+ F}u\text{=}\text{f}\,\text{+}\,\text{{T}'g}\,\text{in}\,\Theta$$

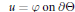$$u=\varphi \,\,on\,\,\partial \Theta$$

The principal part 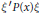${\xi }'P\left( x \right)\xi$ of the above equation is assumed to be comparable to a quadratic form 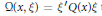$\mathcal{Q}\left( x,\xi \right)={\xi }'Q\left( x \right)\xi$ that may vanish for non-zero 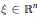$\xi \in {{\mathbb{R}}^{n}}$. This is achieved using techniques of functional analysis applied to the degenerate Sobolev spaces 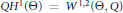$Q{{H}^{1}}\left( \Theta \right)={{W}^{1,2}}\left( \Theta ,Q \right)$ and 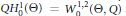$QH_{0}^{1}\left( \Theta \right)=W_{0}^{1,2}\left( \Theta ,Q \right)$ as defined in previous works. E.T. Sawyer and R.L. Wheeden (2010) have given a regularity theory for a subset of the class of equations dealt with here.

Keywords

35A0135A0235D3035J7035H20degenerate quadratic formslinear equationsrough coefficientssubellipticweak solutions.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1395 - 1414
Copyright
Copyright © Canadian Mathematical Society 2012

References

[CRW] Chua, S. K., Rodney, S., and Wheeden, R. L., A compact embedding theorem for generalized Sobolev spaces. arxiv:1110.6907v1.Google Scholar
[FKS] Fabes, E. B., Kenig, C. E., and Serapioni, R. P., The local regularity of solutions of degenerate elliptic equations. Comm. Partial Differential Equations 7(1982), no. 1, 77–116. http://dx.doi.org/10.1080/03605308208820218 Google Scholar
[FP] Fefferman, C. and Phong, D. H., Subelliptic eigenvalue problems. In: Conference on harmonic analysis in honor of Antoni Zygmund, Vol. I, II (Chicago, Ill., 1981), Wadsworth Math. Ser., Wadsworth, Belmont, CA, 1983.Google Scholar
[FSSC] Franchi, B., Serapioni, R., and F. Serra-Cassano, Approximation and imbedding theorems for weighted Sobolev spaces associated with Lipschitz continuous vector fields. Boll. Un. Mat. Ital. B. (7) 11(1997), no. 1, 83–117.Google Scholar
[GL] Gutiérrez, C. E. and Lanconelli, E., Maximum principle, non-homogeneous Harnack inequality, and Liouville theorems for x-elliptic operators. Comm. Partial Differential Equations 28(2003), no. 11–12, 1833–1862. http://dx.doi.org/10.1081/PDE-120025487 Google Scholar
[GT] Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order. Grundlehren der Mathematischen Wissenschaften, 224, Springer-Verlag, New York, 1977.Google Scholar
[MRW] Monticelli, D. D., Rodney, S., and Wheeden, R. L., Boundedness of weak solutions of degenerate quasilinear equations with rough coefficients. Differential Integral Equations 25(2012), no. 1–2, 143–200.Google Scholar
[R1] Rodney, S. W., Existence of weak solutions to subelliptic partial differential equations in divergence form and the necessity of the Sobolev and Poincaré inequalities. Ph. D. Thesis, Mc Master University, Proquest LLC, Ann Arbor, MI, 2007.Google Scholar
[R2] Rodney, S. W., A degenerate Sobolev inequality for a large open set in a homogeneous space. Trans. Amer. Math. Soc. 362(2010), no. 2, 673–685. http://dx.doi.org/10.1090/S0002-9947-09-04809-0 Google Scholar
[SW1] Sawyer, E. T. and Wheeden, R. L., Hölder continuity of weak solutions to subelliptic equations with rough coefficients. Mem. Amer. Math. Soc. 180(2006), no. 847.Google Scholar
[SW2] Sawyer, E. T. and Wheeden, R. L., Degenerate Sobolev spaces and regularity of subelliptic equations. Trans. Amer. Math. Soc. 362(2010), no. 4, 1869–1906. http://dx.doi.org/10.1090/S0002-9947-09-04756-4Google Scholar