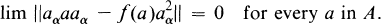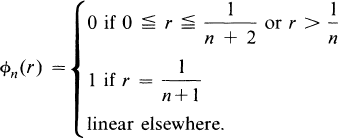Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Akemann, Charles A.
Anderson, Joel
and
Pedersen, Gert K.
1986.
Diffuse sequences and perfect 𝐶*-algebras.
Transactions of the American Mathematical Society,
Vol. 298,
Issue. 2,
p.
747.
Phillips, N.C.
and
Weaver, N.
1998.
Modules with norms which take values in a C*-algebra.
Pacific Journal of Mathematics,
Vol. 185,
Issue. 1,
p.
163.
Kirchberg, E.
and
Phillips, N. Ch.
2000.
Embedding of exact C* -algebras in the Cuntz algebra 𝒪2.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2000,
Issue. 525,
p.
17.
Zacharias, Joachim
2000.
C*-Algebras.
p.
262.
Elliott, George A.
and
Kucerovsky, Dan
2001.
An abstract Voiculescu–Brown–Douglas–Fillmore absorption theorem.
Pacific Journal of Mathematics,
Vol. 198,
Issue. 2,
p.
385.
Rørdam, M.
2002.
Classification of Nuclear C*-Algebras. Entropy in Operator Algebras.
Vol. 126,
Issue. ,
p.
1.
Kucerovsky, Dan
2003.
Extensions contained in ideals.
Transactions of the American Mathematical Society,
Vol. 356,
Issue. 3,
p.
1025.
HAYASHI, TOMOHIRO
2004.
A KISHIMOTO TYPE THEOREM FOR ANTIAUTOMORPHISMS WITH SOME APPLICATIONS.
International Journal of Mathematics,
Vol. 15,
Issue. 05,
p.
487.
Akemann, Charles
and
Weaver, Nik
2004.
Consistency of a counterexample to Naimark's problem.
Proceedings of the National Academy of Sciences,
Vol. 101,
Issue. 20,
p.
7522.
Hamhalter, Jan
2005.
Orthogonal Pure States in Operator Theory.
International Journal of Theoretical Physics,
Vol. 44,
Issue. 7,
p.
839.
Akemann, Charles
and
Weaver, Nik
2007.
Classically Normal Pure States.
Positivity,
Vol. 11,
Issue. 4,
p.
617.
Weaver, Nik
2007.
Set Theory and C*-Algebras.
Bulletin of Symbolic Logic,
Vol. 13,
Issue. 1,
p.
1.
Lin, Huaxin
2007.
Full extensions and approximate unitary equivalence.
Pacific Journal of Mathematics,
Vol. 229,
Issue. 2,
p.
389.
AKEMANN, CHARLES
WASSERMANN, SIMON
and
WEAVER, NIK
2010.
PURE STATES ON FREE GROUP C*-ALGEBRAS.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 1,
p.
151.
Akemann, Charles
Anderson, Joel
and
Tanbay, Betul
2012.
The Kadison–Singer problem for the direct sum of matrix algebras.
Positivity,
Vol. 16,
Issue. 1,
p.
53.
Matui, Hiroki
and
Sato, Yasuhiko
2012.
Strict comparison and $ \mathcal{Z} $-absorption of nuclear C∗-algebras.
Acta Mathematica,
Vol. 209,
Issue. 1,
p.
179.
Ciuperca, A.
Giordano, T.
Ng, P.W.
and
Niu, Z.
2013.
Amenability and uniqueness.
Advances in Mathematics,
Vol. 240,
Issue. ,
p.
325.
Matthew Bice, Tristan
2013.
Filters in C*-Algebras.
Canadian Journal of Mathematics,
Vol. 65,
Issue. 3,
p.
485.
Matui, Hiroki
and
Sato, Yasuhiko
2014.
Decomposition rank of UHF-absorbing C∗-algebras.
Duke Mathematical Journal,
Vol. 163,
Issue. 14,
Pasnicu, Cornel
and
Phillips, N. Christopher
2015.
Crossed products by spectrally free actions.
Journal of Functional Analysis,
Vol. 269,
Issue. 4,
p.
915.