Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T23:18:31.958Z Has data issue: false hasContentIssue false
  • English
  • Français

Even Whitehead Squares are Not Projective

Published online by Cambridge University Press:  20 November 2018

R. James Milgram  and
Peter Zvengrowski
R. James Milgram
Affiliation:
Stanford University, Stanford, California
Peter Zvengrowski
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The projectivity of the Whitehead square wn = [in, in] in π2n-1(SN) has been studied by Randall [6] who proved that if wn is projective then n must be a power of 2 or one less than a power of 2. Here we solve the question in the even case, proving by means of bo homology:

Theorem. 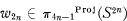if and only if n = 1, 2, 4.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 5 , 01 October 1977 , pp. 957 - 962
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Adams, J. F., Vector fields on spheres, Ann. Math. 70 (1962), 603–632.Google Scholar
2. Hilton, P. J., An introduction to homotopy theory (Cambridge Univ. Press, 1953).Google Scholar
3. Mahowald, M. and Milgram, R. J., Operations which detect Sq4 in connective K-theory, to appear in Trans. A.M.S.Google Scholar
4. Milgram, R. J. and Zvengrowski, P., Skewness of r-fields on spheres, to appear in Topology.Google Scholar
5. Mosher, R. and Tangora, M., Cohomology operations and applications to homotopy theory (Harper and Row, N.Y., 1968).Google Scholar
6. Randall, D., Projectivity of the Whitehead square, Proc. Am. Math. Soc. 40 (1973), 609–611.Google Scholar
7. Randall, D. F-projectivity of the Whitehead square, An. Acad, brasil. Cienc. 17 (1975).Google Scholar