Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:09:39.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates for Solutions of Wave Equations with Vanishing Curvature

Published online by Cambridge University Press:  20 November 2018

Bernard Marshall
Bernard Marshall*
Affiliation:
McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The solution of the Cauchy problem for a hyperbolic partial differential equation leads to a linear combination of operators Tt of the form

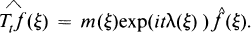
For example, the solution of the initial value problem

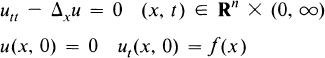
is given by u(x, t) = Ttf(x) where

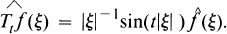
Peral proved in [11] that Tt is bounded from LP(Rn) to LP(Rn) if and only if

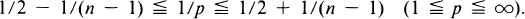
From the homogeneity, the operator norm satisfies ‖Tt‖ ≦ Ct for all t > 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1176 - 1200
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Buchwald, V. T., Elastic waves in anisotropic media, Proc. Roy. Soc. London, Ser. A, 253 (1959), 563–580.Google Scholar
2. Courant, R. and Hilbert, D., Methods of mathematical physics. Vol. II (Interscience Publishers, New York, 1962).Google Scholar
3. Duff, G. F. D., The Cauchy problem for elastic waves in an anisotropic medium, Philos. Trans. Roy. Soc. London, Ser. A, 252 (1960), 249–273.Google Scholar
4. Greenleaf, A., Principal curvature and harmonic analysis, Indiana Math. J. 30 (1981), 519–537.Google Scholar
5. Herz, C., Fourier transforms related to convex sets, Ann. of Math. 75 (1962), 81–92.Google Scholar
6. Hlawka, E., Über Integrale auf konvexen Korpern I, Monatsh. Math. 54 (1950), 1–36; II, ibid. 54 (1950), 81–99.Google Scholar
7. Littmann, W., Fourier transforms of surface-carried measures and differentiability of surface averages, Bull. Amer. Math. Soc. 69 (1963), 766–770.Google Scholar
8. Marshall, B., Strauss, W. and Wainger, S., Lp — Lq estimates for the Klein-Gordon equation, J. Math, pures et appl. 59 (1980), 417–440.Google Scholar
9. Marshall, B., Lp — Lq multipliers of anisotropic wave equations, Indiana Math. J. 33 (1984), 435–457.Google Scholar
10. Marshall, B., The Fourier transforms of smooth measures on hypersurfaces of Rn+1 , Can. J. Math.CrossRefGoogle Scholar
11. Peral, J., Lp estimates for the wave equation, J. Funct. Anal. 36 (1980), 114–145.Google Scholar
12. Strichartz, R. S., Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations, Duke Math. J. 44 (1977), 705–714.Google Scholar
13. Zygmund, A., Trigonometric series (Cambridge U. Press, 1959).Google Scholar