No CrossRef data available.
Article contents
Essentially Convexoid Operators
Published online by Cambridge University Press: 20 November 2018
Extract
Let H be a separable complex Hilbert space and let B(H) denote the algebra of all bounded linear operators on H. Let π be the quotient mapping from B(H) onto the Calkin algebra B(H)/K(H), where K(H) denotes all compact operators on B(H). An operator T ∈ B(H) is said to be convexoid[14] if the closure 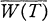 of its numerical range W(T) coincides with the convex hull co σ(T) of its spectrum σ(T). T ∈ B(H) is said to be essentially normal, essentially G1, or essentially convexoid if π(T) is normal, G1 or convexoid in B(H)/K(H) respectively.
of its numerical range W(T) coincides with the convex hull co σ(T) of its spectrum σ(T). T ∈ B(H) is said to be essentially normal, essentially G1, or essentially convexoid if π(T) is normal, G1 or convexoid in B(H)/K(H) respectively.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981


